以下文章來源于Python作業輔導員 ，作者天元浪子

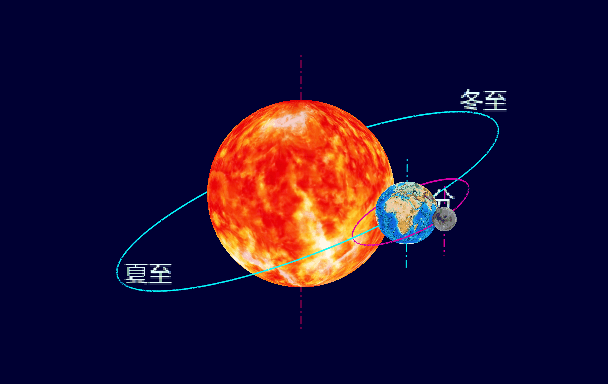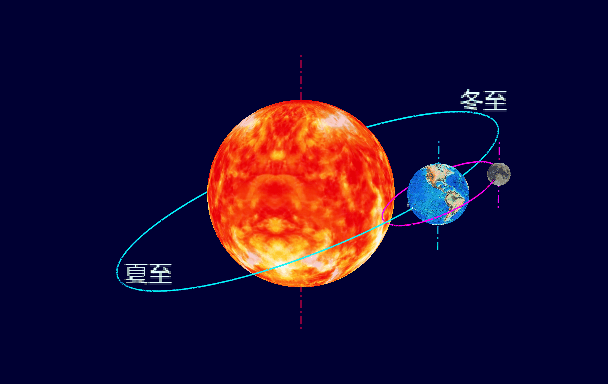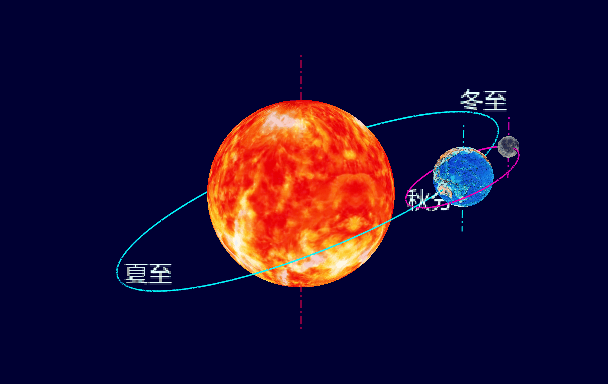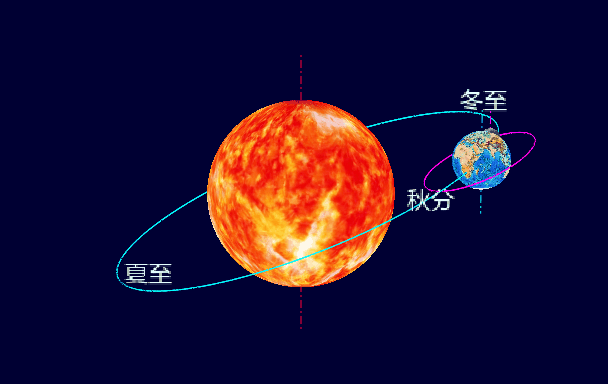
無言相守45億年，太陽、地球和月球這三個好基友究竟是怎樣的關系呢？從孩提時代我就一直在想，要是能有一個可以直觀演示太陽、地球和月球運行軌跡的模型就好了。今天，我終于實現了小時候的夢想：用WxGL畫出了太陽、地球和月球的動態軌道模型。配上簡單的解說，小朋友也可以秒懂四季更迭、日蝕月蝕、黃赤交角。

在開始繪制模型前，讓我們先來了解一下太陽、地球和月球的起源，以及它們的大小、遠近和行蹤路線。

1、主流的大爆炸理論認為，宇宙大爆炸發生在138.17億年前。

2、約66億年前，一顆超新星爆炸后產生了一團星云，逐漸形成了太陽系的雛形。

3、約46億年前，這團星云最中心的巨大氫球，開始產生聚變反應，太陽就此誕生。

4、約45億年前，一顆火星大小的行星“忒伊亞”撞上了地球的雛形，體積增加了近一倍，地球誕生。

5、在這次撞擊中，“忒伊亞”殘骸的一部分形成了月球。

6、太陽半徑696000km，地球半徑6371km，月球半徑1738km，三者之比約為400:3.67:1。

7、太陽繞銀河系中心公轉周期約2.5億年。

8、太陽也在自轉，不過因為是等離子體，所以不同緯度有不同的自轉速度。赤道區域自轉最快，周期為24.47天。

9、地球自轉周期為1天，公轉周期為365.2564天（恒星年）或365.2422天（回歸年）。

10、地球公轉軌道是一個近似圓的橢圓，長半軸為149600000km，短半軸為149580000km，曲率為0.016722。

11、地球自轉軸并不垂直于地球公轉軌道面，地球公轉軌道面（黃道面）與地球赤道面夾角為23.43° 。

12、月球公轉周期為27.32日（恒星月）或29.53天（朔望月），月球自轉周期為27.32日（恒星月）。

13、月球軌道面對黃道面的傾角是5.145°，月球赤道面對黃道面的傾角是1.543°，月球軌道面與月球赤道面夾角為6.688° 。

14、月球軌道是一個橢圓，長半軸為385000km，離心率是0.0549。

15、地球公轉和自轉方向、月球公轉和自轉方向、太陽的自轉方向，是一致的，都是自西向東。

了解了這些，就可以開始繪制模型了。關于WxGL模塊的安裝，請參考我近期的文章，這里不再贅述。下面是完整的代碼，大約一百余行

# -*- coding: utf-8 -*-
import numpy as np
from scipy.spatial.transform import Rotation as sstr
from wxgl import wxplot as plt
R_SUN = 1                           # 以太陽半徑696000km為1個單位
R_EARTH = 30 * 6371/696000          # 地球半徑6371km，此處放大30倍
R_MONTH = 50 * 1738/696000          # 月球半徑1738km，此處放大50倍
A_EARTH = (149600000/696000)/100    # 地球公轉軌道長半軸149600000km，此處縮小100倍
E_EARTH = 0.016722                  # 地球公轉軌道離心率
A_MONTH = 385000/696000             # 月球公轉軌道長半軸385000km
E_MONTH = 0.0549                    # 月球公轉軌道離心率
T = 36                              # 每天36個計數周期
T_SUN_SELF = int(24.47 * T)         # 太陽自轉周期24.47天
T_EARTH_SELF = 1 * T                # 地球自轉周期1天
T_MONTH_SELF = int(27.32 * T)       # 月球自轉周期27.32天
T_EARTH = int(365.2564/3 * T)       # 地球公轉周期365.2564天，此處取1/3
T_MONTH = int(27.32 * T)            # 月球公轉周期27.32天
A_E_ORBIT = 23.43                   # 地球軌道面與地球赤道面夾角
A_M_ORBIT = 23.43 + 5.145           # 月球軌道面與地球赤道面夾角
A_M_EQUATOR = 23.43 - 1.543         # 月球赤道面與地球赤道面夾角
# 地球軌道傾角旋轉器
ROTATOR_E_ORBIT = sstr.from_euler('xyz', (0, -A_E_ORBIT, 0), degrees=True)
# 月球軌道傾角旋轉器
ROTATOR_M_ORBIT = sstr.from_euler('xyz', (0, -A_M_ORBIT, 0), degrees=True)
def rotate_merge(av1, av2):
    """將兩個軸角旋轉合并為一個
    av1         - 元組，首元素（浮點型）為旋轉角度（逆時針為正，右手定則），尾元素（列表或元組）為旋轉向量
    av2         - 元組，首元素（浮點型）為旋轉角度（逆時針為正，右手定則），尾元素（列表或元組）為旋轉向量
    """
    a1, v1 = av1
    a2, v2 = av2
    v1, v2 = np.array(v1), np.array(v2)
    r1 = sstr.from_rotvec(np.radians(a1)*v1/np.linalg.norm(v1))
    r2 = sstr.from_rotvec(np.radians(a2)*v2/np.linalg.norm(v2))
    m = np.dot(r1.as_matrix(), r2.as_matrix())
    r = sstr.from_matrix(m)
    vec = r.as_rotvec()
    phi = np.degrees(np.linalg.norm(vec))
    return phi, vec
def get_ellipse_orbit(a, e, n):
    """計算橢圓軌道，a為長半軸， e為離心率，n為軌道點數"""
    t = np.linspace(0, 2*np.pi, n)
    r = a*(1-e*e)/(1-e*np.cos(t))
    xs = r*np.cos(t)
    ys = r*np.sin(t)
    zs = np.zeros(r.shape)
    return xs, ys, zs
def rotate_s(i):
    """太陽自轉函數：沿Z軸旋轉，T_SUN_SELF個計數周期旋轉一周"""
    return (i%T_SUN_SELF)*360/T_SUN_SELF, (0,0,1)
def rotate_e_orbit(i):
    """地球軌道旋轉函數：沿y軸旋轉23.43°（黃赤夾角）"""
    return -A_E_ORBIT, (0,1,0)
def rotate_e(i):
    """地球自轉函數：沿z軸旋轉，T_EARTH_SELF個計數周期旋轉一周"""
    return (i%T_EARTH_SELF)*360/T_EARTH_SELF, (0,0,1)
def translate_e(i):
    """地球位移函數：T_EARTH個計數周期循環一次"""
    phi = (i%T_EARTH)*2*np.pi/T_EARTH
    r = A_EARTH*(1-E_EARTH*E_EARTH)/(1-E_EARTH*np.cos(phi))
    d = np.array((r*np.sin(phi), -r*np.cos(phi), 0))
    return ROTATOR_E_ORBIT.apply(d)
def rotate_m_orbit(i):
    """月球軌道旋轉函數：沿y軸旋轉28.575°后再跟隨月球自轉"""
    av1 = -A_M_ORBIT, (0,1,0)
    av2 = (i%T_MONTH_SELF)*360/T_MONTH_SELF, (0,0,1)
    return rotate_merge(av1, av2)
def translate_m_orbit(i):
    """月球軌道位移函數：T_EARTH個計數周期循環一次"""
    phi = (i%T_EARTH)*2*np.pi/T_EARTH
    r = A_EARTH*(1-E_EARTH*E_EARTH)/(1-E_EARTH*np.cos(phi))
    d = np.array((r*np.sin(phi), -r*np.cos(phi), 0))
    return ROTATOR_E_ORBIT.apply(d)
def translate_m(i):
    """月球位移函數：T_EARTH個計數周期循環一次"""
    phi = (i%T_EARTH)*2*np.pi/T_EARTH
    r = A_EARTH*(1-E_EARTH*E_EARTH)/(1-E_EARTH*np.cos(phi))
    d1 = np.array((r*np.sin(phi), -r*np.cos(phi), 0))
    d1 = ROTATOR_E_ORBIT.apply(d1)
    phi = (i%T_MONTH)*2*np.pi/T_MONTH
    r = A_MONTH*(1-E_MONTH*E_MONTH)/(1-E_MONTH*np.cos(phi))
    d2 = np.array((r*np.sin(phi), -r*np.cos(phi), 0))
    d2 = ROTATOR_M_ORBIT.apply(d2)
    return d1 + d2
def rotate_m(i):
    """月球自轉函數：T_MONTH_SELF個計數周期旋轉一周"""
    return (i%T_MONTH_SELF)*360/T_MONTH_SELF, (0,0,1)
# 初始化畫布
plt.figure(elevation=5, azimuth=-25)
plt.axis(grid=False)
# 繪制太陽及其自轉軸
plt.sphere((0,0,0), R_SUN, texture='res/sun.jpg', rotate=rotate_s, order='R', light=0)
plt.plot((0,0), (0,0), (1.5,-1.5), color='red', style='dash-dot')
# 繪制地球公轉軌道
xs_e, ys_e, zs_e = get_ellipse_orbit(A_EARTH, E_EARTH, T_EARTH)
plt.plot(xs_e, ys_e, zs_e, color='cyan', width=1, rotate=rotate_e_orbit, order='R')
# 標注冬夏至和春秋分點
i_summer, i_winter = np.argmin(xs_e), np.argmax(xs_e)
i_autumn, i_spring = np.argmin(ys_e), np.argmax(ys_e)
plt.text('夏至', size=32, pos=ROTATOR_E_ORBIT.apply((xs_e[i_summer], ys_e[i_summer], zs_e[i_summer])))
plt.text('冬至', size=32, pos=ROTATOR_E_ORBIT.apply((xs_e[i_winter], ys_e[i_winter], zs_e[i_winter])))
plt.text('春分', size=32, pos=ROTATOR_E_ORBIT.apply((xs_e[i_spring], ys_e[i_spring], zs_e[i_spring])))
plt.text('秋分', size=32, pos=ROTATOR_E_ORBIT.apply((xs_e[i_autumn], ys_e[i_autumn], zs_e[i_autumn])))
# 繪制地球及其自轉軸
plt.sphere((0,0,0), R_EARTH, texture='res/earth.jpg', rotate=rotate_e, translate=translate_e, order='TR', light=0)
plt.plot((0,0), (0,0), (0.5,-0.5), color='cyan', style='dash-dot', rotate=rotate_e, translate=translate_e, order='TR')
# 繪制月球公轉軌道
xs_m, ys_m, zs_m = get_ellipse_orbit(A_MONTH, E_MONTH, T_MONTH)
plt.plot(xs_m, ys_m, zs_m, color='magenta', width=1, rotate=rotate_m_orbit, translate=translate_m_orbit, order='TR')
# 繪制月球及其自轉軸
plt.sphere((0,0,0), 0.1, texture='res/month.jpg', rotate=rotate_m, translate=translate_m, order='TR', light=0)
plt.plot((0,0), (0,0), (0.3,-0.3), color='magenta', style='dash-dot', rotate=rotate_m, translate=translate_m, order='TR')
plt.show()

代碼中用到了太陽、地球和月球的紋理圖片，讀者可自行下載或替換為自己喜歡的圖片。