為了消除兩個電路的差異，對(6)兩邊同乘以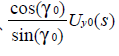得：

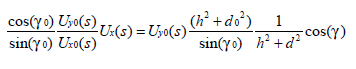
　　記

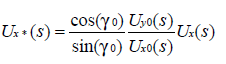
　　對(7)兩邊同乘以0()yUs得：

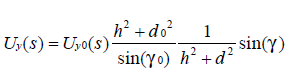
　　記向量。那么U

　　??的方向為，正是載流導線的水平垂直方向，我們用它來判斷載流導線的走勢;而由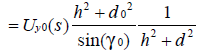得

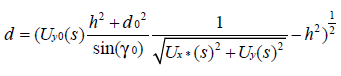
　　1.3 單豎直電感測距

　　如圖4，電感豎直放置，離地高度h。易得

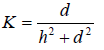
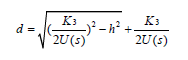　　令運用法一得其中

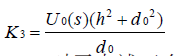
　　對于上述三個模型，我們可以測量一些有代表性的特征量。值得注意的是U0(s)好比一個基準時鐘，是有相位的，但U0(s)和U(s)的相位必然相差0度或180度，具體原因筆者尚不清楚。若電路的輸出電壓無鑒相功能，如峰峰值、有效值、整流濾波輸出值等只有正值，1.1的模型不需擔心該問題，因為小車行進過程中U0(s)和U(s)始終同相，1.2則需通過其他算法判斷導線在小車的左還是右，γ是正還是負，1.3也無法判斷跡線在左還是右。

　　兩個結論

　　以上推導是建立在無限長直導線的基礎上的，但賽道是任意形狀的，且電感會隨著小車擺動，在這種情況下，上述幾個數學模型是否還能適用呢?請看以下兩個結論。

　　結論一：有限長直導線的K也是常數，故對于有限長直導線的循跡，仍可使用上述模型，當然精度會有所下降。對于任意形狀的導線，導線可看作無數段有限長直導線的疊加[5]，所以可以使用上述模型。

　　結論二：對于任意放置的電感，從導線電流到電路輸出電壓之間的傳遞函數，只有K不同，其他部分是一樣的。所以小車行進過程中即使有搖擺，仍可使用上述模型。