削峰填谷最優時基于DSM分時電價的確定與分析
其中:L(t,ξ,Δ)為實行分時電價后, 在給定的ξ和Δ條件下用戶反應后的負荷。
目標函數1用來實現峰負荷最小,目標函數2用來實現谷負荷差最大,目標函數3用來實現峰谷負荷差最小。
從目標函數來看,為了實現削峰填谷最優的目標,進行單目標優化是不夠的,因此選用雙目標優化。觀察目標函數1、2和3,我們可以發現,如果選用目標函數2和另外一個函數進行雙目標優化的話,由于優化的方向不一致,因此進行雙目標優化存在困難;如果選取目標函數1和3進行雙目標優化的話,因為優化方向一致,比較容易解決這個問題。而且,目標函數1和2的優化可以保證削峰填谷最優,因為當峰負荷和峰谷負荷差都最小時,也即是峰負荷最小和谷負荷最大。
多目標優化的方法很多,最簡單和實用的是加權系數法[7]。在加權系數法中,最主要的就是確定權值。由于本文模型是首次提出,缺乏相應的數據和方法,因此,在本文多目標優化過程中,利用權值嘗試法來確定目標函數的權值。
2 仿真與結果比較
本文利用浙江某地區典型日負荷數據進行數值仿真。
2.1 目標函數權值的確定
如前文所述,確定目標函數的權值時采用權值嘗試法,通過比較在目標函數取不同權值時的峰負荷與谷負荷仿真結果來確定目標函數的權值,如表1所示。本文引用地址:http://cqxgywz.com/article/179862.htm
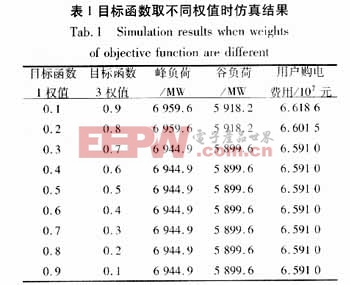
通過比較仿真結果可以看出,目標函數3占的比例比較大時,峰谷負荷差最小,而且峰負荷與實行分時電價前比減少了821.4MW,可以在削峰和填谷之間達到最佳均衡。因此,本文對目標函數1、3的權值取為0.2、0.8。
2.2 仿真算法
(a) 取一平時段電價初值,根據數學模型算出滿足約束條件的平時段電價的上界 和下界;
(b) 從中選出使峰負荷最小和峰谷負荷差最小在權值為0.2、0.8時達到最佳均衡 時的平時段電價;
(c) 算出此平時段電價下的最優拉開度和反應后負荷
2.3 實行分時電價前數據;
(a) 典型日負荷數據如表2所示。
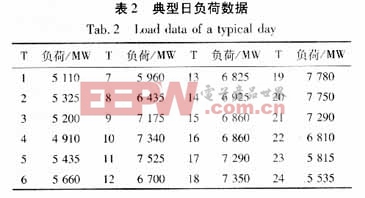
(b) 實行分時電價前最大負荷、最小負荷和用戶購電費用:Lmax=7780MW;Lmin=4910MW;m0=6.6243×107元
2.4 仿真結果
削峰填谷最優時分時電價和用戶反應后負荷數據如下:
ξ=0.360 0,Δ=0.450 0元/kW;Pf=0.677 0元/kW,Pp=0.515 0元/kW,Pg=0.065 0元/kW;k=10.415 4(k為峰時段電價與谷時段電價的比值);Lmax=6 945.6MW;Lmin=5 900.6MW;MTOU=6.573 0×107元。
仿真結果與原始負荷數據比較如圖1所示。
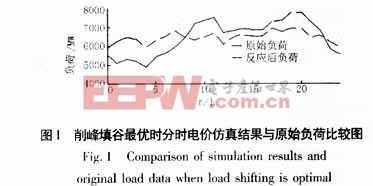
圖1表明,削峰填谷最優分時電價實行后,能夠起到很好的削峰和填谷的作用。從數值上看,削峰填谷最優分時電價實行后,峰負荷為6945.6MW,比實行分時電價前減少了834.4MW,谷負荷為5900.6MW,比實行分時電價前增加了990.6MW。
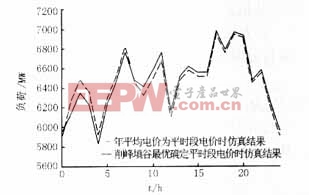
2.5 與文獻[5,6]仿真結果比較
本文仿真結果和文獻[5-6]仿真結果如表3和圖2所示。







評論