量子比特:一只又死又活、不死不活的薛定諤貓
然而,真做這個實驗的時候,我們竟出人意料地得到紅色和藍色的電子(見圖8)。這簡直是不可思議的結果:測量又紅又軟的電子的“顏色”時,我們居然有一半的幾率會看到藍色。(當然另一半的幾率會看到紅色)。類似地,如果我們再次測量 |藍軟〉這束又藍又軟的電子的“顏色”時,實際上我們也會看紅色和藍色(見圖8),和對 |紅軟〉的觀測結果一模一樣。真是實驗越多越糊涂。
本文引用地址:http://cqxgywz.com/article/201903/398750.htm
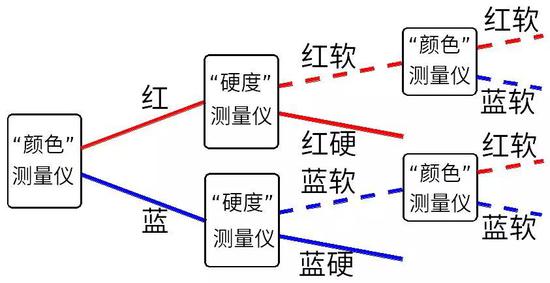
圖8:先測量電子的“顏色”,接著測量電子的“硬度”,最后再測量電子的“顏色”。這是我們實際得到的結果。 為了把這個問題搞清楚,讓我們做更多的實驗。進一步的實驗表明,如果我們對 |紅軟〉和 |藍軟〉這兩束電子做相同的測量,我們總是得到完全相同的結果。|紅軟〉和 |藍軟〉這兩種狀態是完全不可區分的。我們應該認為它們是同一個態:|紅軟〉=|藍軟〉。
仔細觀察圖8,我們發現,測量紅色電子的“硬度”后,會得到軟電子和硬電子。可是當我們再測量軟電子的顏色時,我們發現這個軟電子忘了它原來是個紅電子,變成了一個顏色不確定的電子。所以圖8中把這個電子叫做 |紅軟〉是不合適的,因為它其實沒有確定的顏色。類似地,當我們測量藍色電子的“硬度”后,也會得到軟電子和硬電子。但這個軟電子也會忘了它原來是個藍電子,變成了一個顏色不確定的電子。這個從藍電子得到的軟電子和從紅電子得到的軟電子,一模一樣,不可區分。原來顏色的信息完全丟掉了。所以圖8中的標記是不正確的。我們應當把它重新畫成下面的圖9。
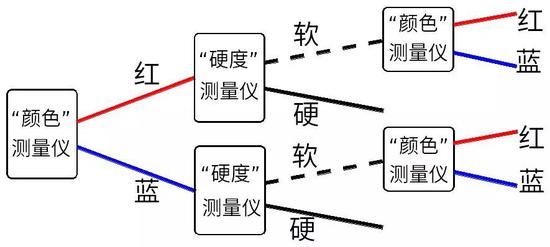
圖9:先測量電子的“顏色”,接著測量電子的“硬度”,最后再測量電子的“顏色”。這是我們實際得到的結果和正確的標記。
更一般地講,不管進入“硬度”測量儀的電子是處于什么樣的態,經“硬度”測量儀分離出來的軟態總是同一個態,分離出來的硬態也總是同一個態。類似的,不管進入“顏色”測量儀的電子是處于什么樣的態,經“顏色”測量儀分離出來的紅態總是同一個態,分離出來的藍態也總是同一個態。
這種對電子自旋的測量和研究,揭示了我們量子世界中的測不準原理。“顏色”(自旋豎分量)和“硬度”(自旋橫分量)有一個互不相容的性質。如果一個電子有了確定的“硬度”,那么它就沒有確定的“顏色”。如果它有確定的“顏色”,那它就沒有確定的“硬度”。對“硬度”的測量會影響電子的“顏色”,對“顏色”的測量會影響電子的“硬度”(見圖9)。
當然“顏色”和它自己是相容的。也就是說如果我們測量“顏色”以后再測量“顏色”,我們會得到同樣的顏色。多次測量顏色,不會改變一個電子的顏色(見圖10)。
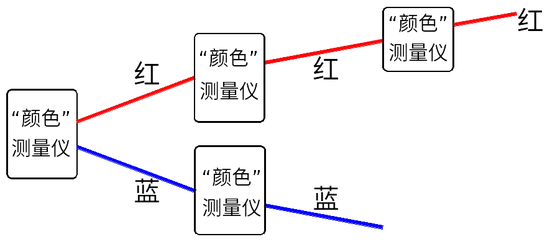
圖10:多次測量顏色,不會改變電子的顏色。
通過圖6的實驗,我們把一束電子分成四束。我們想試圖說明電子有不同“顏色”不同“硬度”的四種狀態。可是根據上面所描寫的更多實驗,我們發現圖6這四束電子中,有兩束代表同一個狀態。另外兩束代表另一個相同狀態。所以最后我們只得到兩種不同的狀態。所以圖6對測量的描述不太準確。更準確地描述由圖11所示。
把四個態“裝”到兩個態里:量子疊加態
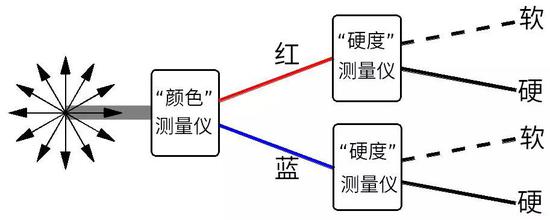
圖11:測量電子的“顏色”之后,再接著測量電子的“硬度”。雖然這樣把一束電子分成四束,但其只代表兩種不同狀態。
圖11中我們用了四個標志 |紅〉,|藍〉 , |軟〉,|硬〉來標志電子的自旋態。這是不是說明電子有四個態?這里我們想說明,在經典圖像中,物體狀態這個概念有一個相互排斥的性質。也就是說,一個體系如果有兩個可能的狀態A和B,那就意味著如果體系處于A態,那就一定不處于B態;如果體系處于B態,那它一定不處于A態。
通過圖10所示的實驗觀察,我們發現如果測量紅電子的顏色,我們只能得到紅色而得不到藍色;如果測量藍電子的顏色,我們只能得到藍色而得不到紅色。這說明 |紅〉、|藍〉這兩個態有相互排斥的性質。也就是說一個紅電子一定不是藍電子;一個藍電子也一定不是紅電子。類似的,|軟〉、|硬〉這兩個態也有相互排斥的性質。一個軟電子一定不是硬電子;一個硬電子也一定不是軟電子。我們這里好像在說廢話。
可是 |紅〉態和 |軟〉態就沒有相互排斥的性質。如圖9所示,如果我們測量紅電子的硬度,我們有時候會感到軟,說明 |紅〉態和 |軟〉態不相互排斥;我們有時候也會感到硬,這說明 |紅〉態和 |硬〉態也不相互排斥。類似的,|藍〉態和 |軟〉,|硬〉態也都沒有相互排斥的性質。這種相互不排斥狀態的存在是量子世界中的新現象,是經典理論中沒有的概念。這也是量子理論詭異的起源。
從圖11中我們看到,|紅〉態中含有 |軟〉態也有 |硬〉態。所以當我們測量紅電子的硬度時,我們發現它是一個又軟又硬的電子。但顯然一個紅電子不是一個軟電子,也不是一個硬電子。所以我們說紅電子是一個又軟又硬不軟不硬的電子:它是一個微觀的薛定諤貓。數學上我們把 |紅〉態記為:|紅〉= |軟〉+ |硬〉。這就是量子理論中疊加態的概念:|紅〉態是 |軟〉態和 |硬〉態的疊加。圖9就是逼出這一概念的實驗。
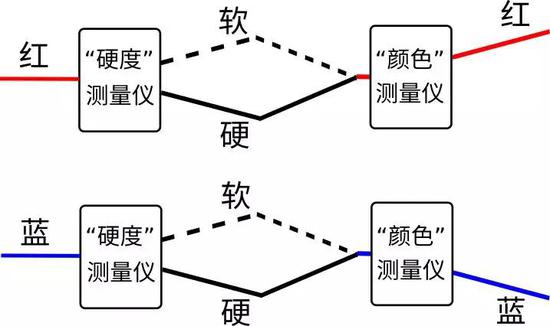
圖12:當我們把從一束紅電子中得出的軟電子和硬電子重新結合起來之后,我們又會重新得到紅電子。類似地,如果我們把從一束藍電子中得出的軟電子和硬電子重新結合起來,我們會重新得到藍電子。
量子疊加不僅僅是一個抽象的數學概念,它也是一個可以在實驗室中實現的實際操作(見圖12)。我們上面說過,一束紅電子通過“硬度”測量儀可以分裂為一束軟電子和一束硬電子。如果用反射鏡把這束軟電子和這束硬電子重新結合起來,我們居然重新得到一束紅電子!這不是科學幻想。這是在實驗室中實際觀測到的結果,這就是我們奧妙神奇的量子世界,這就是我們為什么把紅態表示為:|紅〉= |軟〉+ |硬〉。
從圖11我們又看到 |藍〉態也是一個又軟又硬不軟不硬的態。我們也想把 |藍〉態記為:|藍〉= |軟〉+ |硬〉。但這樣 |紅〉和 |藍〉就完全一樣了。這是不可接受的,因為 |紅〉和 |藍〉明明是完全不同、而且相互排斥的態。為區別 |紅〉和 |藍〉,我們把 |藍〉態記為:|藍〉= |軟〉- |硬〉。這樣 |藍〉態是 |軟〉態和 |硬〉態的一個不同的疊加,其中疊加系數有個負號。
上面我們利用 |紅〉和 |藍〉來描寫自旋 |上〉和 |下〉兩個態。我們利用 |軟〉和 |硬〉來描寫自旋 |左〉和 |右〉兩個態。下面我們將回到自旋的語言。這樣關系 |紅〉= |軟〉+|硬〉和 |藍〉= |軟〉- |硬〉就變成 |上〉= |左〉+ |右〉和 |下〉= |左〉- |右〉。這說明 |上〉態是一個又左又右、不左不右的態。|下〉態也是一個又左又右、不左不右的態。通過這兩個關系,我們可以得到 |左〉= 2(|上〉+ |下〉)~ |上〉+ |下〉和 |右〉= 2(|上〉- |下〉)~ |上〉- |下〉(在這里,系數2被忽略了,見下節)。所以 |左〉態是一個又上又下、不上不下的態。也是一個薛定諤貓態。我們這種對自旋態的量子看法滿足空間90度旋轉對稱性。
什么是量子比特?
在經典物理中,最簡單的系統就是一個比特。一個比特只有兩個態:0和1。比如我們可以把0和1這兩個態看作是上面所講的自旋|上〉,|下〉兩個態。而量子疊加原理告訴我們:任何兩個態的疊加也是一個可能的態。所以一個量子比特,不僅有|0〉和|1〉兩個態,還有它們的任意疊加態:
|ψ〉= ψ0 |0〉+ ψ1 |1〉
這里ψ0 和 ψ1 是兩個復數,被稱為疊加系數。我們發現一個量子比特可以有無窮多個不同的狀態,這些狀態由兩個復數 ψ0 和 ψ1 來刻畫。當然這無窮多個態大多都不是相互排斥的。我們最多有兩個相互排斥的態,如 |0〉和 |1〉,|0〉+ |1〉和 |0〉- |1〉,等等。
為什么疊加系數必須是復數?這也是一個非常深刻的問題。我們知道自旋的指向是三維的。不僅有上下左右四個方向。還有前后兩個方向。自旋 |前〉態是一個不上不下又上又下態,也是一個不左不右又左又右的態。我們想把 |前〉態寫為 |前〉= |上〉+ |下〉。但這是不對的。因為 |上〉+ |下〉已被用來表示 |左〉態。我們發現只有引入復數 i,才能把 |前〉態表示為 |上〉|下〉的疊加態:|前〉= |上〉+ i|下〉。類似的自旋向后的 |后〉態是 |上〉|下〉的另外一個疊加態:|后〉= |上〉- i|下〉。這樣 |前〉態是一個不上不下又上又下態,也是一個不左不右又左又右的態。|后〉態是另一個不上不下又上又下態,也是另一個不左不右又左又右的態。所以我們的量子世界要求我們用復數來刻畫物質的各種各樣量子態。
其實事情還沒有這么簡單。這兩個復數對量子比特狀態的刻畫不是一一對應的,而是多對一的。兩對復數 (ψ0 , ψ1) 和 (ψ‘0 , ψ‘1) 其實描寫的是同一個量子態,如果它們之間有如下關系的話:
ψ0 = cψ‘0 ,ψ1 = cψ‘1
其中,c 是一個任意的復數。所以一個量子比特不同的態對應于一個球面上的點。這就是量子比特狀態的布洛赫球表征(圖13)。經典比特1和0兩種狀態對應于南北兩極,而量子比特可以處在這兩種態的任意疊加態上,由球面上的其它點表示。這些點表達了這么一個又不是0又不是1,但又是0又是1的虛無縹緲的狀態。在量子世界中好像連邏輯這一基本推理工具都要被修正了。
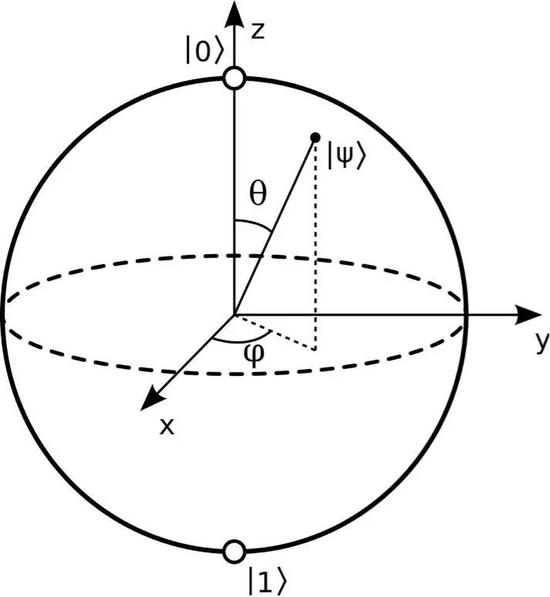
圖13:布洛赫球:一個量子比特不同的量子態,一一對應于一個球面上的點。我們可以用一個電子的兩個自旋態,來實現一個量子比特:自旋向上對應于0態,自旋向下對應于1態。那么自旋向上和自旋向下的疊加態,也就是球面上的其他點,對應于自旋指向那個方向的量子態。比如 |↑〉- |↓〉是一個指向水平x方向的自旋態 |→〉,而 |↑〉- |↓〉是一個指向水平反x方向的自旋態 |←〉。自旋向上的態 |↑〉也可以看成是 |→〉和 |←〉兩個態的疊加: |↑〉= |→〉+ |←〉。
如果我們把1和0兩種狀態看著是自旋上下兩種狀態,那么布洛赫球表征就描寫了自旋指向各個不同方向的量子態。我們對自旋的量子描寫是滿足空間任意角度旋轉對稱性的。
上面我們講了一個電子的自旋有兩種(相互排斥的)狀態,其正好實現了一個量子比特。其實光子也有自旋,一個光子的自旋也有兩種(相互排斥的)狀態,我們也可以用它來實現了一個量子比特。實際上量子通訊就是用光子的自旋——這個量子比特——來實現的。
我們知道光有偏振現象。光的偏振可以有不同的方向,代表了光子自旋的不同的狀態(見圖14)。這無窮多個偏振方向,表示光子自旋可以有無窮多個不同的狀態。但像電子自旋一樣,這無窮多個態大多都不是相互排斥的。我們最多有兩個相互排斥的態,如豎偏振和橫偏振。我們可以用豎偏振代表0,用橫偏振代表1。這樣一個光子的自旋(偏振態)就是一個量子比特。一個光子還可以有左斜偏振,其對應于一個又橫又豎不橫不豎的偏振態,記為 |0〉+ |1〉。一個光子也可以有右斜偏振,其對應于另一個又橫又豎不橫不豎的偏振態,記為 |0〉- |1〉。有一種量子加密通訊就是利用這四種狀態的光子來實現的。
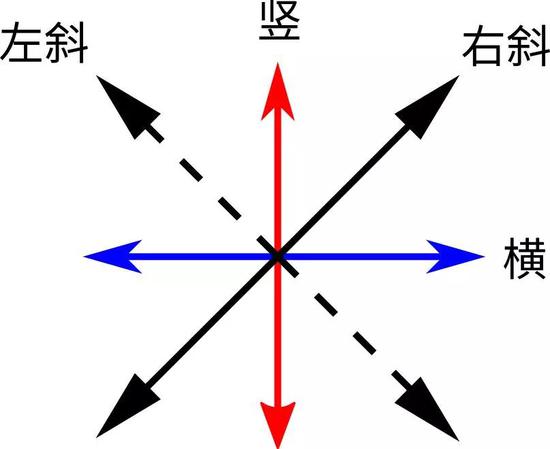
圖14:一個光子可以有很多偏振態,如豎偏振,橫偏振,左斜偏振,右斜偏振,等等。
量子比特這不是0不是1,又是0又是1奇怪的狀態便是有名的“活貓死貓悖論”的來源。想象在一個密封的盒子中,有一只貓、一瓶毒藥、一個榔頭,和一個量子比特探測器(圖4)。我們給探測器一個量子比特,讓其測量。如果量子比特是處于1態的話,榔頭就會落下,放出毒藥,我們就會得到一只死貓。如果量子比特是處于0態的話,榔頭就不會落下,貓還是活的。如果量子比特是處于0和1的一個疊加態,那么過了一段時間,這只貓到底是死的還是活的?按照量子理論,這只貓應該是處于一個不死不活,又死又活的狀態。而這種狀態的貓被稱之為薛定諤貓(圖15)。

圖15 :如何把一只可愛的貓,變成一只薛定諤貓
當我們了解薛定諤貓之后,我們就可以了解量子通訊。如果我們只用0態和1態,這兩種相互排斥的狀態來傳遞信息的話,那么我們做的就是經典通訊。如果我們用0態和1態,再加上亦0亦1、非0非1的兩個態 |0〉+ |1〉和 |0〉- |1〉,這4個相互不排斥的量子態來傳遞信息的話,那我們做的就是一種形式的量子通訊。以后我們會有文章進一步詳細介紹這種形式的量子通訊。
在這篇文章里我用盡量貼近實驗的角度,來描寫量子存在和量子疊加原理。我想讓讀者感覺到這一量子新概念是如何被實驗逼出來的。這一實驗角度正巧和一個非常抽象的數學描寫——范疇學理論——非常接近。其實范疇學并不是一門抽象的數學語言,而是一門非常貼近實驗的語言,是很值得做物理的學生來掌握的語言。另外我個人對現有的量子理論很不滿意,覺得它不是描寫我們世界最終正確的理論。要發展出超越量子力學的理論,也許范疇學會起一個關鍵作用。



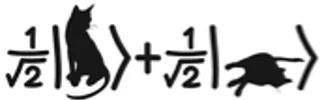

評論