Mathematica入門教程之Mathematica的基本語法特征
加入技術交流群
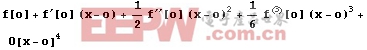
In[3]:=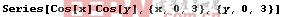
Out[3]:=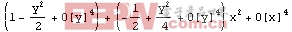
. 常微分方程
求解常微分方程和常微分方程組的函數的一般形式如下:
Dsolve[eqns,y[x],x] 解y(x)的微分方程或方程組eqns,x為變量
Dsolve[eqns,y,x] 在純函數的形式下求解
NDsolve[eqns,y[x],x,{xmin,xmax}] 在區間{xmin,xmax}上求解變量x的數的形式下求解常微分方程和常微分方程組eqns的數值解
In[1]:=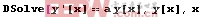
Out[1]:=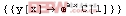
In[2]:=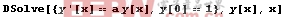
Out[2]:=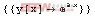
In[3]:=
Out[3]:=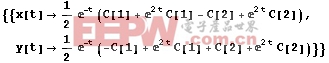
.線性代數
- 定義向量和矩陣函數
- 矩陣的運算符號和函數
- 方程組求解函數
定義一個矩陣,可用函數Table或Array.當矩陣元素能用一個函數表達式時,用函數Table在定義矩陣大小的同時也給每個矩陣元素定義確定的值.用函數Range只能定義元素為數值的向量.Array只能用于定義向量、矩陣和張量,并規定矩陣和張量的元素下標從1開始.Array的一般形式: Array[向量元素名,n,f] 定義下標從f開始的有n個元素的向量,當f是1時可省略. Array[矩陣元素名,{m,n}] 定義m行n列的矩陣.其中:矩陣元素名是一個標識符,表示矩陣元素的名稱,當循環范圍是{u,v,w}時定義一個張量. Table[表達式f,循環范圍] 表達式f表示向量或矩陣元素的通項公式;循環范圍定義矩陣的大小. 循環范圍的一般形式:{循環變量名,循環初值,循環終值,循環步長}. 在Array或Table的循環范圍表示方法略有區別.請在下面的實例中注意觀察.
In[1]:=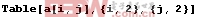
Out[1]:=
(*矩陣每一行元素用一對{}括起來*)
In[2]:=
Out[2]:=
In[3]:=
(*IndentityMatrix[n]生成n維矩陣*)
Out[3]:=
評論