當所有的儲能元件均沒有初始儲能，電路處于零初始狀態情況下，外加激勵在電路中產生的響應稱為零狀態響應。

下面分別討論激勵為直流、正弦交流情況下，、電路的零狀態響應。

一、直流激勵下的零狀態響應。

1、串聯電路

如圖8-5-1所示，開關S原置于位置2，電路已達穩態，即，電容上無初始儲能。在時刻，開關S由2切換至1，電路接通直流電壓源，求換路后的零狀態響應、、。

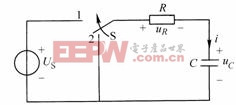
圖8-5-1

當，開關S切換至1，由得：

（式8-5-1）

這是一個一階線性常系數非齊次微分方程。由微分方程求解的知識得，特解：

齊次方程的通解：

全解為：

（式8-5-2）

根據換路定則：

由（式8-5-2）：

因此：

最終求得：

（式8-5-3）

（式8-5-4）

（式8-5-5）

根據（式8-5-3）—（式8-5-5），畫出零狀態響應、與隨時間變化的曲線，如圖8-5-2所示。

圖8-5-2

在圖8-5-1所示電路中，當后，電壓源對電容充電。電容從初始電壓為零逐漸增大，最終充電至穩態電壓，而電流則從初始值逐漸減小，最終衰減至穩態值零。

2、串聯電路。

如圖8-5-3所示，開關S置于位置2，電路已達穩態，即，電感L上無初始儲能。在時刻，開關S由2切換至1，電路接通直流電壓源，求換路后的零狀態響應、和。

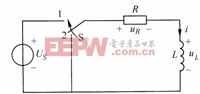
圖8-5-3

當后，開關S切換至1，由得：

（式8-5-6）

（式8-5-6）是一個一階線性常系數非齊次微分方程。該方程的全解是特解和齊次方程的通解之和，即：

（式8-5-7）

表示全解，表示特解，表示通解。換路后電路達到新的穩定狀態的穩態電流就是特解，即：

（式8-5-8）

其通解為：

（式8-5-9）

于是，全解為：

（式8-5-10）

（式8-5-10）中的積分常數A由初始條件確定。在時刻，根據換路定則：

由（式8-5-10）：

因此：

最終得到：

（式8-5-11）

（式8-5-12）

（式8-5-13）

顯然，，滿足。圖8-5-4繪出了零狀態響應、和的曲線。

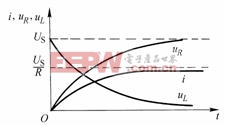
圖8-5-4

二、正弦交流激勵下的零狀態響應

1、串聯電路

仍以圖8-5-1所示電路為例，將直流電壓源改為正弦交流電壓源，當后，由得到電路的微分方程為：

（式8-5-14）

的全解等于特解和通解之和，即：

由于激勵是正弦交流激勵，即為穩態分量，即為暫態分量。穩態分量可利用相量計算：

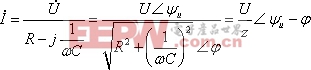
式中 ：

暫態分量仍為，于是全解為：

（式8-5-15）

當時刻，根據換路定則，確定積分常數：

由（式8-5-15）：

最終得到：

（式8-5-16）

（式8-5-17）

（式8-5-18）

（式8-5-16）～（式8-5-18）說明電源的初相角對暫態分量的大小有影響，通常稱為接通角。當或時，電容電壓的暫態分量為最大。從（式8-5-16）不難看出，電容過渡電壓的最大值無論如何不會超過穩態電壓幅值的兩倍。但是從（式8-5-17）可以看出，在某些情況下，過渡電流的最大值將大大超過穩態電流的幅值。

2、RL串聯電路

仍以圖8-5-3所示電路為例，將直流電壓源改為正弦交流電壓源，當后，由KVL得到電路的微分方程為：

（式8-5-19）

初始條件仍是。如前所述，非齊次微分方程的全解是特解與通解之和，即：

（式8-5-19）右邊是正弦函數，特解也是正弦函數，特解就是正弦交流激勵下的穩態電流，可用相量求解：

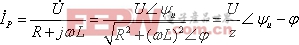
式中：

，

（式8-5-20）

暫態電流仍為：

（式8-5-21）

于是全解為：

（式8-5-22）

根據換路定則：

由（式8-5-22）：

因而：

最終得到：

（式8-5-23）

（式8-5-24）

（式8-5-25）