本節介紹拉普拉斯變換（也稱為拉氏變換）的基本性質，了解掌握了這些性質，可以更加方便地求解各種拉普拉斯正反變換。

一、線性定理

設 則：

（式9-2-1）

式中為常系數。

例9-2-1 求、和的拉氏變換。

解：

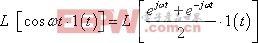
同理：

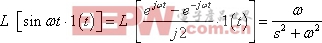
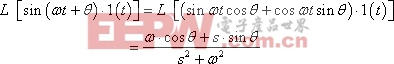
二、微分定理

設 ，則：

（式9-2-1）

同理可推廣得到的高階導數的拉氏變換式：

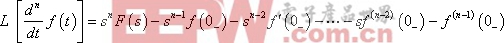
例9-2-2：

已知，求。

解：由于，由（式9-2-2）得：

同理：

三、積分定理

設，則：

（式9-2-3）

例9-2-3 求。

解：斜坡函數是單位階躍函數的積分，由（式9-2-3）得：

四、時域位移（延時）定理

設，則：

（式9-2-4）

例9-2-4：求圖9-2-1所示函數的拉普拉斯變換式。

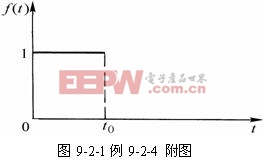
解：由圖可知：

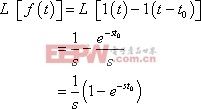
五、復頻域位移定理

設，則：

（式9-2-5）

例9-2-5：已知

求：和的拉普拉斯反變換。

解：利用復頻域位移定理：

六、卷積定理：

設，則：

（式9-2-6）

例9-2-6．求的拉普拉斯反變換式。

解：已知，利用卷積定理得：

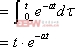
同理可推得：

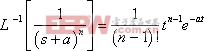
七、初值定理

設，則

例9-2-7．設，驗證初值定理。

解：

又：

，所以，得證！

八、終值定理：

設，則

例9-2-8．仍設，驗證終值定理。

解：

，又

所以，得證!

注意：利用終值定理求的前提條件是必須存在，且是唯一確定的值。