圖9-5-1(a)所示是一個RLC串聯電路，初始條件是、，利用上一節的電路元件及其模型，可畫出相應的復頻域電路模型，即運算電路，如圖9-5-1(b)所示。

圖9-5-1

根據復頻域的KVL，得到：

令，則上式寫為：

式中稱為RLC串聯電路的運算阻抗，其例數稱為運算導納。正弦穩態電路中RLC串聯阻抗是，形式上與相似。

應用拉普拉斯變換分析線性動態電路過渡過程的方法，通常被稱為運算法。

下面請看幾個例題。

例9-5-1 圖9-5-2(a)所示電路，開關閉合前處于零狀態，試求電路。

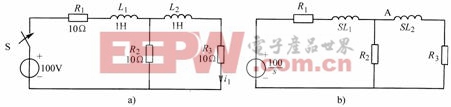
圖9-5-2例9-5-1附圖

解：因為電路原處于零狀態，畫出其運算電路的如圖9-5-2(b)所示，采用戴維南定理，求AB以左電路的戴維南等效電壓：

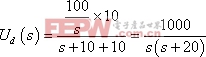
等效運算阻抗：

故電流的象函數：

最后求原函數：

例9-5-2 如圖9-5-3（a）所示，

開關K在位置1時電路處于穩態，在時將開關置于位置2，求。

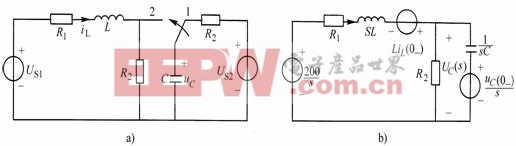
如9-5-3例9-5-2附圖

解：當t＜0時，開關位于“1”且電路處于穩態，則：

，

作運算電路如圖9-5-3（b）所示，由節點電壓法：

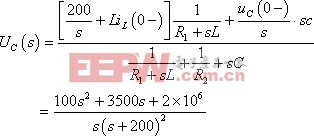
將作部分分式展開并求出相應系數得：

最后得原函數：

例9-5-3 并聯電路如圖9-5-4（a）所示，換路前電路處于零狀態，電流源為單位沖激函數，試求和。

圖9-5-4例9-5-3附圖

解：作運算電路如圖9-5-4（b）所示：

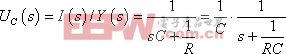
原函數：

，

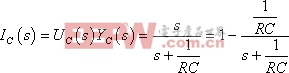
原函數：