只含一個非線性項的超混沌系統及其電路實現
1.2 系統的Lyapunov指數
Lyapunov指數是定量描述混沌吸引子的相鄰軌線收縮或擴張的量,混沌系統和超混沌系統很難區分,可以通過系統的Lyapunov指數來區分。由參考文獻[7]可知,對于一個四維自治的系統,在它的4個Lyapunov指數中,當最大Lyapunov指數為零,其他Lyapunov指數為負時,系統是周期的;當2個最大的Lyapunov指數都為零,其他Lyapunov指數為負時,系統是偽周期的;當最大的Lyapunov指數為正,其他3個Lyapunov指數中有1個為零,其余為負時,系統是混沌的;當有2個最大的Lyapunov指數為正,其他2個Lyapunov指數中有1個為零,有1個為負時,系統是超混沌的。運用Matlab計算出系統(1)的Lyapunov指數,當t→∞時,系統(1)的4個Lyapunov指數為:λL1=0.101 4,λL2=0.014 0,λL3=0,λL4=-0.646 2。由此可知系統(1)是一個超混沌動力系統。
1.3 超混沌系統Poincare映射圖
Poincare映射是一種經典的分析動力系統的技術,可以通過Poincare截面上截點的情況判斷是否發生混沌:當Poincare截面上有且僅有一個不動點或少數離散點時,運動是周期的;當Poincare截面上是一封閉曲線時,運動是準周期的;當Poincare截面上是一些成片的具有分形結構的密集點時,運動是混沌的。系統(1)在z=0截面的Poincare映射圖如圖5所示。
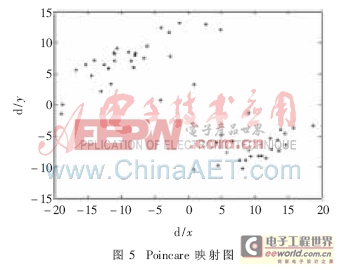
從圖5中可以觀察到截面上是一些成片的具有分形結構的密集點,可以明確知道系統是混沌的,從而也驗證了1.2中的判斷。
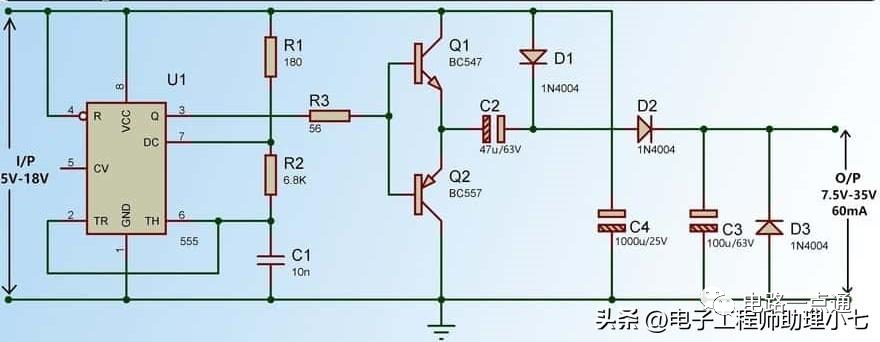
2 系統混沌模型電路仿真
對超混沌系統(1)的電路進行了詳細推導,得到超混沌的電路數學模型為:




評論