2 TT-VGT機器人的位姿逆解

　　TT-VGT（Tetrahedron-Tetrahedron-Variable Geometry Truss）機器人是由多個四面體組成的變幾何桁架機器人,平面ABC為機器人的基礎平臺,基本單元中各桿之間由球校連接,通過可伸縮構件li(i=1,2,…n)的長度,來改變機構的構形,如圖2所示。

　　設冗余度TT-VGT機器人操作手由N個伸縮關節組成,圖3所示為兩個單元的TT-VGT構成。設變量qi(i=1,2,…N)為平面ACB和平面BCD的夾角,其相應的速度和加速度分別為qi,qi(i=1,2,…N)。

　　它們與li,li,li(i=1,2,…N)的關系如下[1]：

　　式中,d表示TT-VGT中不可伸縮構件的長度

　　li,l''i,l''''I分別表示機器人可縮構件的長度、速度和加速度

　　相鄰兩個四面體單元的坐標系的建立如圖3所示。坐標系XiYiZi相對于坐標系Xi-1Yi-1的變換矩陣可表示為：

　　對于機構自由度為N、任務自由度為L的冗余度TT-VGT機器人,其余四面體單元的結構與坐標系的建立與圖3所示的相似。由文獻[1]可知,其末端位姿X是中間變量qi(i=1,2,…,N)的函數,有：

　　X=f(q)　　 (3)

　　對式（3）求導,可得如下的運動學方程式：

　　X=Jq　　 （4）

　　式中,X=(x1,x2,…,xL) T∈R L

　　q=(q1,q2,…,qN)T∈R N

　　LN

　　J為機器人的雅可比矩陣,

　　由式（4）可得：

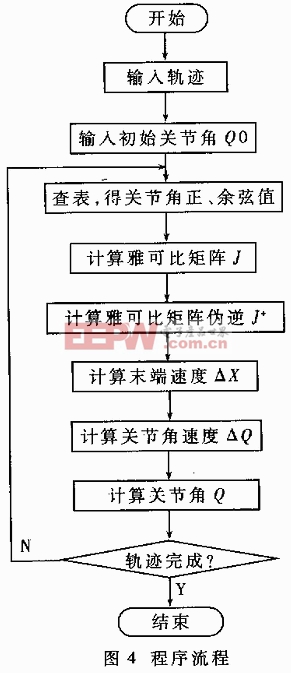
　　q=J + X (6)

　　式中,J+為雅可比矩陣的偽逆,

　　J+=J T(JJT)-1 (7)

　　將式(6)離散化,可得機器人運動軌跡上第k點各關節中間變量的dqk及位置qk：

　　dqk=J+dXk (8)

　　q k=q (k-1)+dq k (9)

　　將q k代入式（1）,可求得TT-VGT機器人各伸縮構件的長度li。