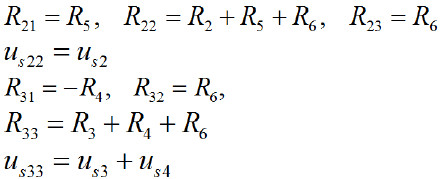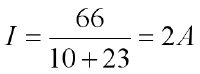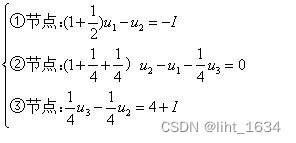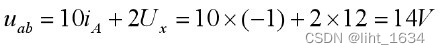電路原理分析-清華于歆杰
目錄:
一、KCL與KVL
1、定義
2、例題
二、電壓源、電流源、受控源性質
1、獨立電源
2、受控電源
3、計算要點★
4、支路電流法
5、節點電壓法
6、網孔電流法
7、疊加定理
8、戴維南與諾頓定理
9、例題
三、電壓電流源的應用
1、電流源等效
2、電橋電路
3、雙電源供電
四、阻抗和導納、相量法
1、復數
2、電阻/電感/電容的阻抗
3、相量圖(Phasor Diagram)★
4、復阻抗與復導納
5、例題
五、正弦交流電路的功率
1、瞬時功率
2、平均功率
3、最大功率傳輸★
4、無功功率和視在功率
5、視在功率
6、功率因素
7、復功率
六、對稱三相電路計算
1、三相電源與三相電路
七、線性電路的過渡分析
1、線性電路的過渡過程
2、1階電路的零輸入響應
3、1階電路的零狀態響應
附錄
1、電子運動方向
一、KCL與KVL
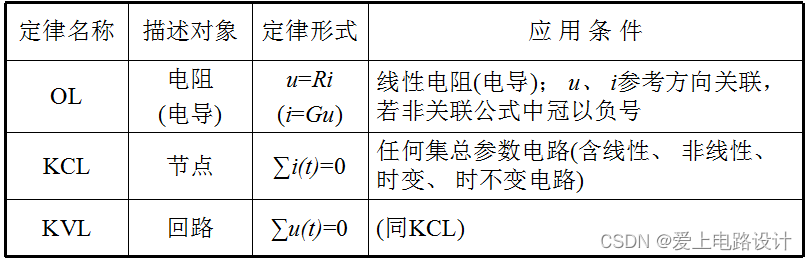
1、定義
1)基爾霍夫電流定律
電路中任一個節點上,在任一時刻,流入節點的電流之和等于流出節點的電流之和。
通常規定,對參考方向背離(流出)節點的電流取正號,而對參考方向指向(流入)節點的電流取負號。廣泛使用的參考方向的符號約定稱之為無源符號約定。
對閉合曲面 S,有 i1+i2-i3 = 0A。若兩部分電路只有一根線相連(1 或 5 或 6 其中一個),由 KCL 可知,該支路中無電流。
如圖(b)所示電路,作閉合曲面 S,因只有一條支路穿出 S 面。根據 KCL,由于 i1、i2、i3 只能有一個且 i1+i2-i3 = 0A,故 i = 0。
2)基爾霍夫電壓定律
沿著閉合回路所有元件兩端的電勢差(電壓)的代數和等于零。
電流方向與巡回方向一致取正,電流方向與巡回方向相反取負;遇到電壓降低的電源取正;遇到電阻上的電壓降低(實際上習慣的電流是與巡回方向一致的),當然也取正。
從 a 開始定義為正,U1 與 U5 的下方為正(如圖),此時 U4 要一并處理,U4 下方為正。那么:
U1+U2+U3-U4-U5 = 0V,-U3-Ux+U5+U4 = 0V。
2、例題
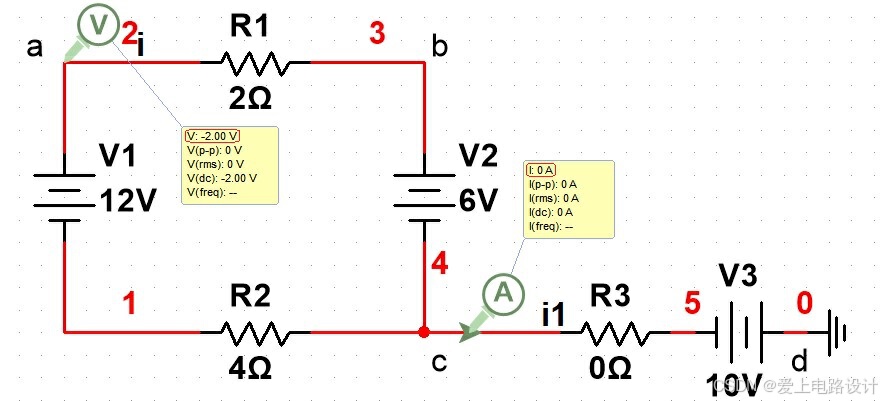
題1、已知 R1 = 2Ω,R2 = 4Ω,Us1 = 12V,Us2 = 10 V,Us3 = 6V,求 a 點電位 Va。
圖1.2.1 KCL例題
本題 d 點為參考點,由 KCL 可知 i1 = 0,所以回路 A(藍色框)各元件上流經的是同一個電流i;
由 KVL 列寫方程 R1*i+Us3+R2*i-Us1 = 0V,代入己知的各電阻及理想電壓源的數據,得 i = 1A;
求解電位 Va,就是求 a 點到參考點的電壓,它是自 a 點沿任一條可以到“地”的路徑而“走”到“地”,沿途各段電路電壓的代數和,所以有 Va = Uab+Ubc+Ucd = 2*i+6+(-10) = 2Ω*1A+6V-10V = -2V。
圖1.2.2 KCL例題仿真
題2、已知 I = 0.3A,求解電阻 R 的阻值。
解:
如圖所示,c 點電壓 = 0.3*20 = 6V,Uac = 12V-6V = 6V,I1 = 6V/15 = 0.4A
根據 KCL 得:I1 = I2+0.3A,I2+I3 = IR,解得 I2 = 0.1A
根據 KVL 從 a 點開始沿圖上虛線得:12V-UR-2V-6V = 0,UR = 4V,注:電流方向與巡回方向相反取負
那么,I3 = (12V-4V)/20 = 0.4A,則 IR = 0.4A+0.1A = 0.5A
故 R = 4V/0.5A = 8Ω
二、電壓源、電流源、受控源性質
1、獨立電源
獨立電源分為電壓源與電流源,電源的參數有電壓、電流、方向。
電壓源(內阻為零,電壓變化量 Δu = 0 相當于短路)與電流源或電阻并聯,輸出電壓不變,如果所求參數與電流源、電阻無關,則電流源、電阻可以開路處理。
電流源(內阻無窮大,電流變化量 Δi = 0 相當于開路)與電壓源或電阻串聯,輸出電流不變,如果所求參數與電壓源、電阻無關,則電壓源、電阻可以短路處理。
電壓源的電壓屬性、電流源的電流屬性是定值,不受外電路影響,淺顯易懂的理解請移步:。
因為與電源的定義矛盾,電壓源不能短路,電流源不能開路;不同電壓的電壓源不能并聯,不同電流的電流源不能串聯;參數相同則合并成一個電源。
此外,電流源與電壓源可以等效轉換,一個電流源與電阻并聯可以等效成一個電壓源與電阻串聯。電源互換等效在推廣應用中要特別注意等效端子。
1)任意電路元件與理想電壓源Us并聯
任意電路元件包含理想電流源元件。
2)任意電路元件與理想電流源Is串聯
任意電路元件包含理想電壓源。
3)電壓源、電流源互換等效
4)T型到π型轉換電路分析
對于圖 (a)、(b)電路,根據 KCL 得:i3 = i1+i2 ①
根據 KVL 從(b) 圖1 點開始得:U12+U23-U13 = 0V,U12 = U13-U23
由(a) 圖,根據 KVL,則有:U13 = R1*i1+R3*i3,U23 = R2*i2+R3*i3 ②
將 ① 式代入 ② 式,可得:U13 = (R1+R3)i1+R3*i2,U23 = R3*i1+(R2+R3)i2
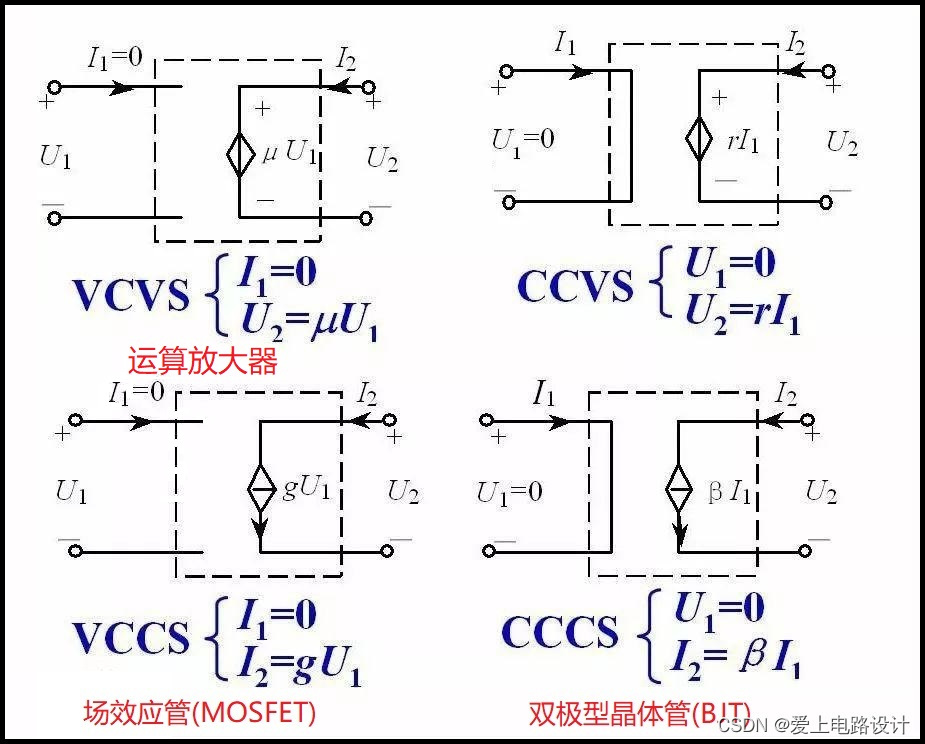
2、受控電源
受控電源具有相應電源的屬性,只是其參數受激勵源控制,受控電源是非獨立電源。這里的參數就包含方向,所以受控源標注的方向只是參考方向,實際方向由激勵源控制。受控電壓源與受控電流源進行等效變換時要保留激勵源不變。
例1:求 ab 端開路電壓 Uoc。
解:
設電流 I1 參考方向如圖中所標,由 KCL,得 I1 = 8I+I = 9I
對回路 A 應用 KVL 列方程得 2I+2I1-20V = 0V
將代入式,解得 I1 = 9A
由歐姆定律得開路電壓 Uoc = 2I1 = 2*9 = 18V
Multisim仿真:
例2:求 ab 端的輸出電阻 Ro。
解:
外施電壓源u, 求電流 i; 外施電流源 i, 求電壓 u(注意:所設 u、i 的參考方向對二端電路來說是關聯的),則其等效電阻 Rab = u/i。
在ab端外施電流源 i, 設電壓 u 使 u、i 對二端電路來說參考方向關聯, 并設電流 i1、i2 參考方向如(b)圖上所標。
u1 = 15*i1,i2 = u1/10
∴ i2 = (15/10)*i1 = 1.5*i1 又 i1+i2 = i
∴ i1 = (1/2.5)*i
由 KVL 列回路 A 的 KVL 方程:5*i+15*i1-u = 0
即 5*i+15*(1/2.5)*i = u
所以輸出電阻:Ro = u/i = 11Ω
電源置零時電壓源短路處理,電流源開路處理,受控源不能直接置零。
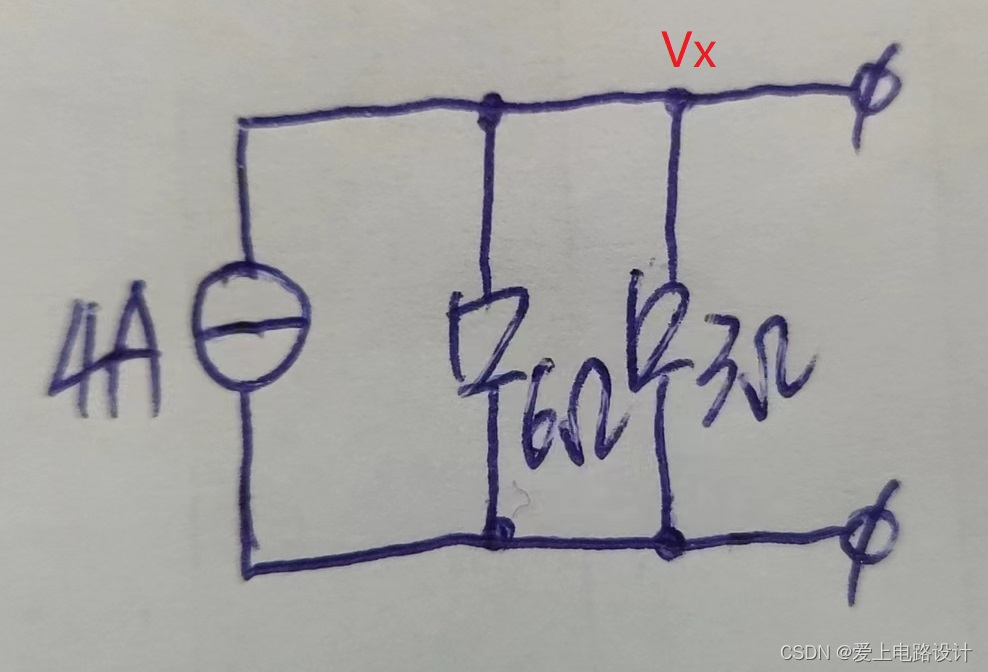
例題:簡化電路并求解 Uab 的電壓。
圖2.3.1 電路簡化例題
Is/4A 電流源開路處理,R1/10Ω 不起作用。V1/24V、V2/12V、V3/4V 電壓源短路處理,R4/3Ω 不起作用。簡化后的電路如圖2.3.2 所示。
圖2.3.2 變換后的電路
Vx = 4A*(6Ω//3Ω) = 8V,Uab = 8V+4V = 12V。
圖2.3.3 例題仿真
電流參考方向確定后,電路中元件的電壓降方向(+ → -)與電流參考方向一致的,稱為關聯方向;相反,則是非關聯方向。
“元件”包含電源,而電動勢的方向是負極指向正極,與電壓方向相反,這里容易出錯,要把電源看成元件!
在討論元件功率問題時,關聯方向的元件,功率為正是吸收功率;功率為負是發出功率。正值是得到,負值是付出,符合常理,思考很順暢。而非關聯方向正相反,別扭。
解題時先求出實際的電壓、電流,功率的符號按關聯方向賦值。
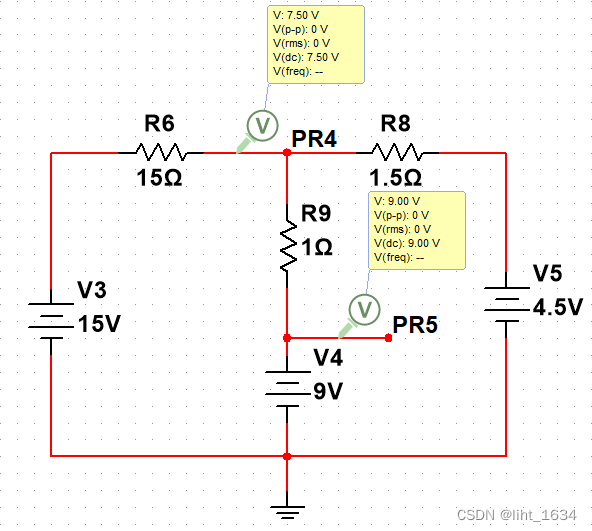
4、支路電流法已知 R1 = 15Ω,R2 = 1.5Ω,R3 = 1Ω,Us1 = 15V,Us2 = 4.5V,Us3 = 9V。求電壓 Uab 及各電源產生的功率。
圖2.4.1 支路電流法例題
解:
設支路電流 i1、i2、i3 參考方向如圖中所標。依 KCL列寫節點 a 的電流方程為 i1+i3 = i2
選網孔作為獨立回路,并設繞行方向于圖上,由 KVL 列寫網孔的電壓方程分別為
網孔 15i1-i3 = 15V-9V
網孔 i3+1.5i2 = 9V-4.5V,解得 i1 = 0.5A,i2 = 2A,i3 = 1.5A
電壓 Uab = -i3*1+Us3 = 7.5V
設電源 Us1、Us2、Us3 產生的功率分別為 Ps1、Ps2、Ps3,由求得的支路電流,可算得
Ps1 = Us1*i1 = 15*0.5 = 7.5W
Ps2 = -Us2*i2 = -4.5*2 = -9W
Ps3 = Us3*i3 = 9*1.5 = 13.5W
圖2.4.2 例題仿真
5、節點電壓法節點電壓法是以流入節點的電流代數和為零列方程的,基本規則如下:
自電導之和乘以節點電壓,減去互電導乘以相鄰節點電壓,等于流入節點的電源電流代數和。
自電導:只要電阻的一端在節點上,電阻的倒數就是電導。互電導:電阻連接在兩個節點之間。電流源內阻無窮大,電導為零。
受控源只是參數受激勵源控制,其電源屬性不變。必要時無伴電壓源轉換成兩端電壓是定值的電流源。
Proteus仿真:
支路電流法和節點電壓法典型例子:
網孔電流法是假設電流沿著網孔流動,電流的方向可以任意設定,可以預估一下真實的方向,盡量避免答案是負值,比較麻煩。
列方程時沿著網孔電流方向,網孔電流乘以網孔總電阻是正值,通過公共電阻的相鄰網孔電流,方向相同取正值,反之取負值,電壓源也是如此。電壓源的代數和放在方程右邊。
圖2.6.1 網孔電流法例題
按網孔列寫 KVL 方程如下:
網孔 A:R1*iA+R5*iA+R5*iB+R4*iA-R4*iC+Us4-Us1 = 0;
網孔 B:R2*iB+R5*iA+R5*iB+R6*iB+R6*iC-Us2 = 0;
網孔 C:R3*iC-R4*iA+R4*iC+R6*iC+R6*iB-Us4-Us3 = 0;
按未知量順序排列并加以整理,同時將已知激勵源也移至等式右端。這樣整理改寫上述 3 式得:
觀察 (2.2-1) 式,可以看出:
iA 前的系數 (R1+R4+R5) 恰好是網孔 A 內所有電阻之和,稱它為網孔 A 的自電阻,以符號 R11 表示。
iB 前的系數(+R5)是網孔 A 和網孔 B 公共支路上的電阻,稱它為網孔 A 與網孔 B 的互電阻,以符號R12表示,由于流過 R5 的網孔電流 iA、iB 方向相同,故R5 前為“+”號。
iC 前系數(-R4)是網孔 A 和網孔C 公共支路上的電阻,稱它為網孔A 與網孔 C 的互電阻,以符號 R13表示,由于流經 R4 的網孔電流iA、iC 方向相反,故 R4 前取“-”號。
等式右端 Us1-Us4 表示網孔 A 中電壓源的代數和,以符號 Us11 表示, 計算 Us11 時遇到各電壓源的取號法則是,在巡行中先遇到電壓源正極性端取負號,反之取正號。
用同樣的方法可求出 (2.2-2)、(2.2-3) 式的自電阻、互電阻及網孔等效電壓源,即:
疊加定理的概念即對于一個線性系統,一個含多個獨立源的雙邊線性電路的任何支路的響應(電壓或電流),等于每個獨立源單獨作用時的響應的代數和,此時所有其他獨立源被替換成他們各自的阻抗。
簡單來說在一個電路中,當電壓源作用時,電流源為斷路;當電流源作用時,電壓源為通路。
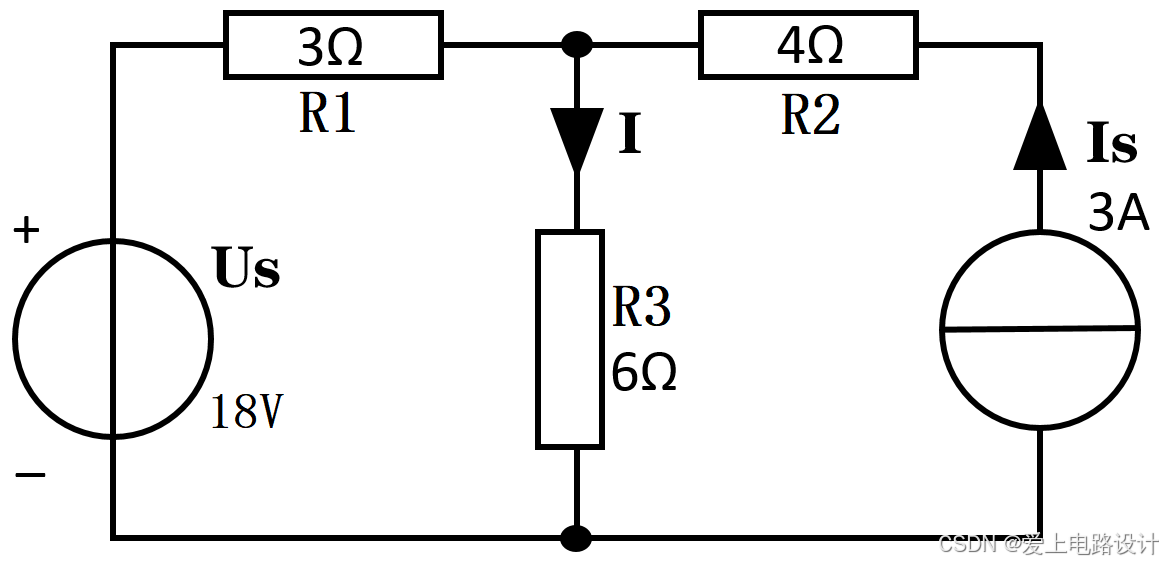
例題:用疊加定理求如圖2.7.1 所示電路中的電流 I,Us 為 18V。
圖2.7.1 疊加定理例題
圖中有一個電流源和一個電壓源共同作用,我們需要使用疊加定理來計算電流中的I,電流 I 為電壓源 Us 和電流源 Is 共同作用的結果,所以我們需要分析兩種情況。
首先我們將電阻進行命名容易更好的來展示電流的方向,R1 = 3Ω,R2 = 4Ω,R3 = 6Ω。
第一種情況,當電壓源 Us 作用時,Is為斷路。我們可將電路簡化為圖2。
電流的方向為:從 Us 的正極→R1→R3→回到 Us 的負極。
根據中學的串聯電路定理可求出I的大小,I = U/R = Us/(R1+R3) = 18V/(3Ω+6Ω) = 2A。
那么電流的走向:從上往下流,電流的大小為:2A。
圖2.7.2 回路1
第二種情況,當電流源 Is 作用時, Us 為通路,我們可將電路簡化為圖2.7.3。
電流 Is 有兩條線路,分別為:
①從Is出發→R2→R1→回到 Is
②從Is出發→R2→R3→回到 Is
根據并聯電路分流定理我們可計算出I的大小,I = Is*(R1/(R1+R3)) = 3A*(3Ω/(3Ω+6Ω)) = 1A
那么電流的走向:從上往下流,和第一種情況下的電流方向一致。
圖2.7.3 回路2
由上述兩種情況我們可知,在電壓源和電流源共同作用下電流 I 的方向都為從上往下流,那我們可將得出的 1、2 中電流I相加得到最終的結果。圖2.7.1 中的電流 I = 2A+1A = 3A。
分析完上題后,下面假設電流 Is 方向相反,于是得到的電路如圖2.7.4。
圖2.7.4
我們依然需要做兩種分析:
電壓源作用時,依舊和圖2 一致,I 的大小還是為 2A。
但電流源的作用就有些許的差別了,我們可以畫出電流源作用的圖2.7.5。
圖2.7.5
電流 Is 有兩條線路。
①從 Is 出發→R3→R2→回到 Is
②從 Is 出發→R1→R2→回到 Is
電流流經 R3 是與所求電流的方向為反向,那么我們求取得電流將為負值。
根據并聯電路分流定理我們可計算出I的大小,I = -(Is*(R1/(R1+R3) = -(3A*(3Ω/(3Ω+6Ω)) = -1A
由兩種情況我們可知,在電壓源和電流源共同作用下電流I的方向都為從上往下流或從下往上流,可得出的 1、2 中電流 I 相加得到最終的結果。圖2.7.4 中的電流 I = 2A+(-1A) = 1A。
溫馨提示:在計算疊加定理時不只要考慮大小并且需要考慮方向。
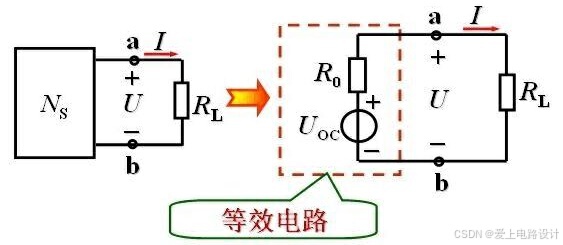
8、戴維南與諾頓定理可以將復雜的有源線性二端電路等效為一個電壓源與電阻串聯的電源模型。
圖2.8.1 等效變換
電壓源的電壓等于有源二端網絡 N 在負載開路時的電壓 Uoc;串聯電阻 R0 等于有源二端網絡內所有獨立電源置零(獨立電壓源短路、獨立電流源開路)時,得到無源二端電路 N 的端口等效電阻。
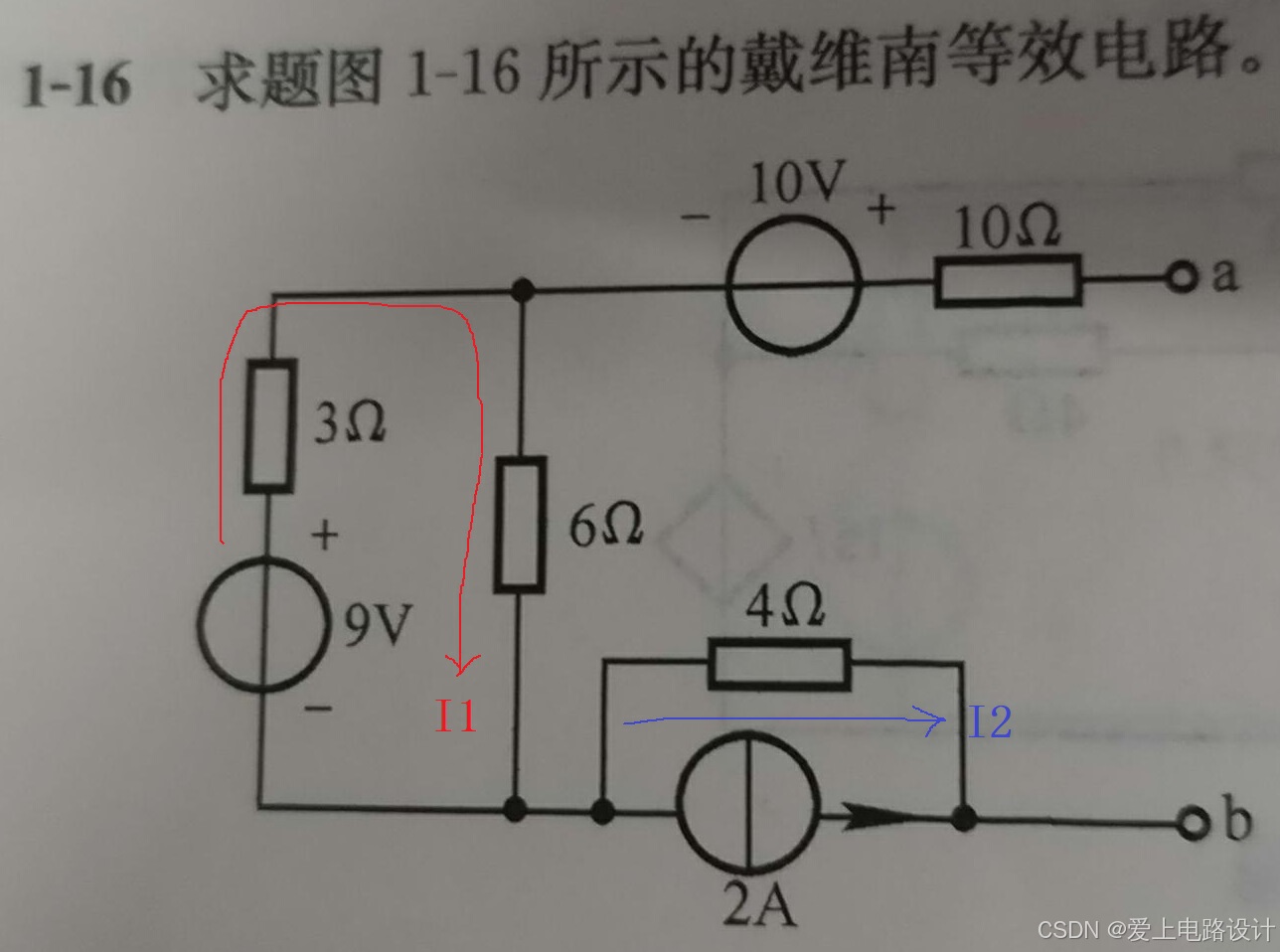
圖2.8.2 戴維南等效例題
根據題目:
(1)先求開路電壓
電流回路只有兩個,如圖2.8.2。
第一個電流回路 I1 = 9V/(3Ω+6Ω) = 1A,
第二個電流回路 I2 = 2A,
所以 Uoc = -I2*4Ω+I1*6Ω+10V = -2A*4Ω+1A*6Ω+10V = 8V。
(2)再求等效電阻
將電壓源短路,電流源開路,可得 3Ω 和 6Ω 并聯,再與 10Ω、4Ω 串聯,即 R0 = 10Ω+3Ω*6Ω/(3Ω+6Ω)+4Ω = 16Ω。
諾頓定理:可以將復雜的有源線性二端電路等效為一個電流源與電阻并聯的電源模型。電流大小等于原電路短路時端口流過的電流,電阻也是等于全部獨立源置 0 時的等效電阻。
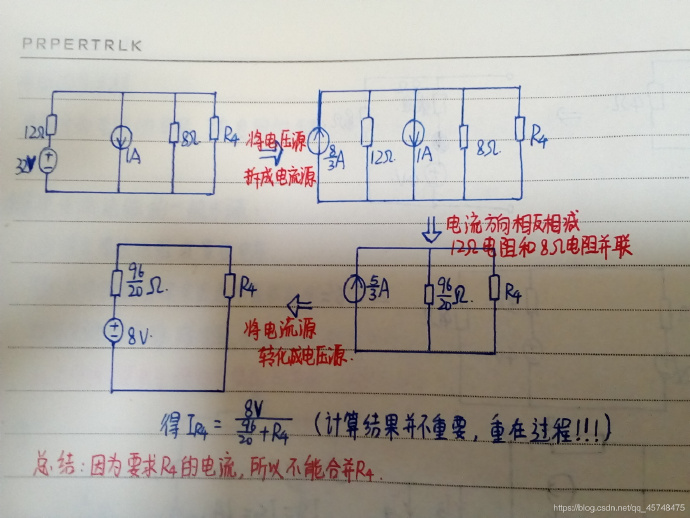
9、例題例1、求 b 點電位 Vb。
應用電阻并聯等效、電壓源互換為電流源等效,將(a)圖等效為(b)圖。再應用電阻并聯等效與電流源并聯等效,將(b)圖等效為(c)圖。 由(c)圖應用分流公式求得:
例2、求電流 I。
應用任意元件(也可是任意二端電路)與理想電壓源并聯可等效為該電壓源及電源互換等效,將(a)圖等效為(b)圖,再應用理想電壓源串聯等效,將(b)圖等效為(c)圖。由(c)圖算得:
例3、求各參數。
解:
受控電流源的電流方向、兩端的電壓方向(極性)是由激勵源控制的。圖中標示的是參考電流方向。如圖,設 2A 電流源電壓為 U2 ,受控電流源電壓為 U3:
u1 = 2 * 5 = 10V
I1 = 0.05 * u1 = 0.5A
U2 = u1 - 3 = 7V
U3 = 3 + 20 * I1 = 13V
各元件的功率:
電壓源 P1 = - 1.5 * 3 = - 4.5W
電流源 P2 = - 2 * 7 = - 14W
受控源 P3 = - 0.5 * 13 = - 6.5W
三個電源共發出功率 25 瓦,電阻吸收功率 P = 2 * 10 + 0.5 * 0.5 * 20 = 25W。
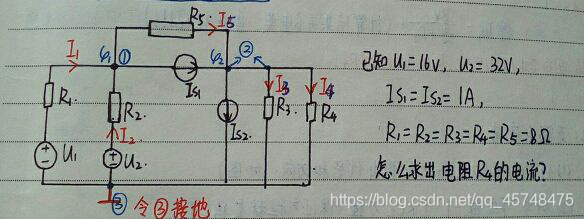
例4、求如圖所示電路節點電壓 U1、U2、U3。
解:
由歐姆定律得:U1 = 2A*2Ω = 4V
對于回路 A 做 KVL: 4V-U2+U2-U3+i*1 = 4V 解得 U3 = i
對于回路 B 做 KVL: 2*I+U1-U2+U2-U3 = 4V 解得 U3 = 2I
∴i = 2I
對回路再做 KCL: 1+I = i 連立式解得:I = 1A,i = 2A
∴U3 = 2V
對于回路 C 做 KVL:2i+(4-U2)/2 = 1
∴U2 = 10V
最后得 U1 = 4V,U2 = 10V,U3 = 2V
例5、用節點分析法求圖示電路中電壓 U1、U2 和 U3。
解:列寫節點方程
電路如圖所示,假設流過電壓源支路的電流為 I,則其節點方程如下:
補充方程:u3-u1 = 24V
聯立求解可得:u1 = 8V,u2 = 0V,u3 = 32V。
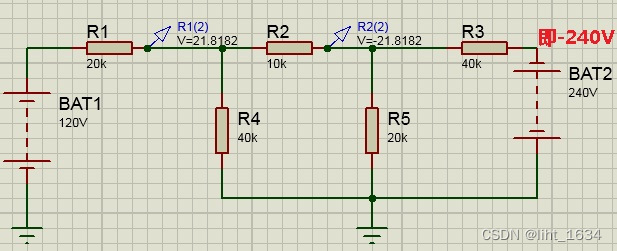
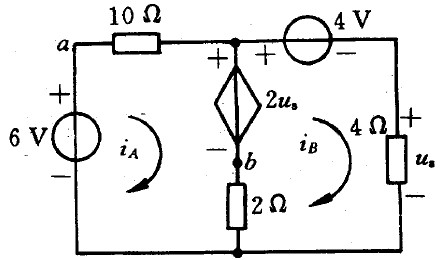
例6:使用網孔電流法求下方電路中的電壓 Uab。
設網孔電流 iA、iB 如圖中所標,觀察電路,應用方程通式列基本方程為:
由圖可以看出控制量 Ux 僅與回路電流 iB 有關,故有輔助方程:
將上面 2 式化簡整理,得:
解得:
所以:
例7:求 a、b 電壓。
解:
通過右側的方程可得 a ≈ 5.685,b ≈ 6.949,與上面的仿真結果相符。
三、電壓電流源的應用
1、電流源等效
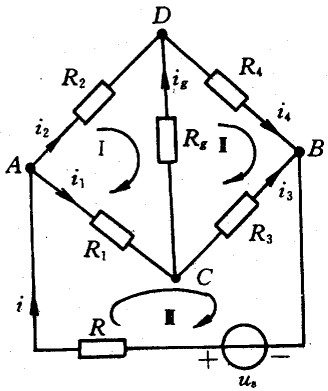
AB 支路為電源支路,CD 支路為橋路,試用支路電流法求電流 ig,并討論電橋平衡條件。
對于節點 A i1+i2-i = 0
對于節點 C -i1+ig+i3 = 0
對于節點 D -i2-ig+i4 = 0
對于回路 -R1i1+R2i2-Rgig = 0
對于回路 -R3i3+R4i4+Rgig = 0
對于回路 R1i1+R3i3+Ri = us
解上述方程組,得:
當 ig = 0,即橋路上電流為零(或橋路兩端電壓:uCD = 0)時稱該電橋達到平衡。由ig的表示式可知分母是有限值,因而僅當 R3 = R1*R4/R2,即 R1/R2 = R3/R4 時 ig = 0,這就是電橋平衡的條件。
圖3.3.1 雙電源供電仿真
開關電源 V1 由 V1 與 D1 組成,開關電源 V2 由 V2 與 D2 組成,當 S1 閉合后,V1 已經不再給負載 R1、R2 供電,由 V2 供給。
四、阻抗和導納、相量法在二維平面上的一個相量,乘以j逆時針旋轉 90°,除以j或乘以-j順時針旋轉 90°;乘以 -1 正時針或逆時針旋轉 180°。
相量畫法原則:
1)同頻率正弦量的相量,才能表示在同一張相量圖中
2)逆時針旋轉,正角度增加的方向
3)選定一個參考相量(設其初相位為零,水平線方向)
相量 IL = 相量 IC+IR,Ldi/dt = 1/C∫idt+IR,即 jωL = 1/jωC+IR(jω 用相量替換掉瞬時值)。
例1:
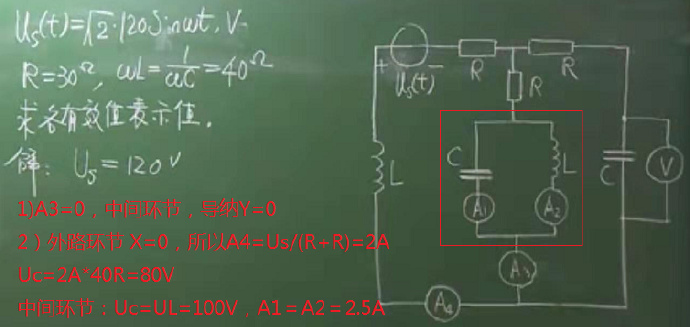
注:如果ωL = 80R,那么UC = 2A*80R = 160V,此時元件上的電壓大于電源的電壓(交流電路)。
五、正弦交流電路的功率
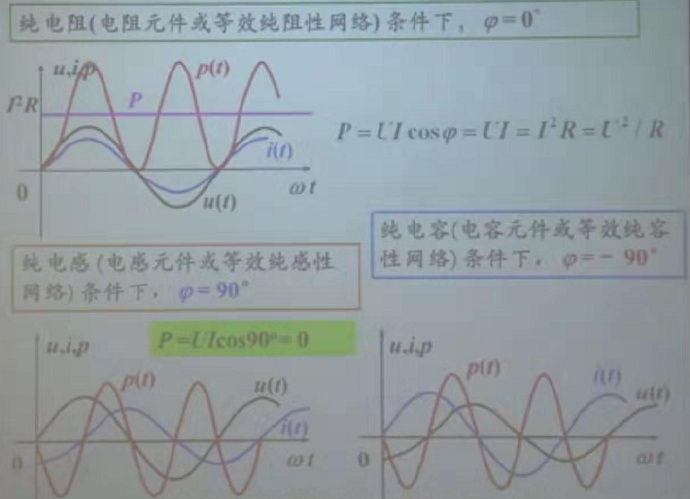
1、瞬時功率
3、最大功率傳輸★
1)直流電源的最大功率
原文件:
2)交流電源的最大功率七、線性電路的過渡分析
1、線性電路的過渡分析
在一定激勵的情況下,任何系統的響應的狀態都有相對穩定和不穩定兩種狀態。在電路中,達到穩定狀態是指在給定條件下電路中電壓、電流已達到穩定值。不穩定狀態是指電壓、電流隨時間在發生動態變化。例如:電容、電感 的充電過程。
穩定狀態(穩態):電路中所有的響應或是恒定不變,或是按周期規律變化的工作狀態。
過渡過程(動態、暫態):在某個激勵下,電路由一個穩態轉變到另一個穩態的過程。這種轉變一般說來不是即時完成的,需要一個過程,這個過程稱為電路的過渡過程。
產生暫態的原因:
內因:電路為動態電路,即電路中含儲能元件 L、C ,能量只能連續變化而不能躍變;
外因:存在外部激勵,如電路換路,即開關通斷、電源變化、元件參數變化等。
分析過渡過程的方法:電路方程是以電流、電壓為變量的微分方程。因此,暫態的分析有兩種方法:
時域分析法:以時間作為變量,直接求解微分方程的方法。
復頻域分析法:采用積分變換求解微分方程的方法。例如通過拉普拉斯變換,將自變量轉換為復頻率變量。
2)換路換路:電路受到新的激勵,具體地講如電路中支路的接通、切斷、短路或電路參數的突然改變及電路連接方式改變的統稱。在進行理論分析時,我們假設換路是即時完成的。定義以下三個時刻:
t = 0 表示換路時刻(計時起點);
t = 0- 表示換路前的一瞬間(換路尚未發生);
t = 0+ 表示換路后的一瞬間(換路已經發生)。
儲能元件中能量的改變是需要時間的。即動態電路在換路后一般不能由原來的穩定狀態立刻到達新的穩定狀態。
圖7.1.1 電容儲能
圖7.1.2 電感儲能
在換路瞬間,當電容元件的電流為有限值時,電容電壓一般不能躍變;當電感元件的電壓為有限值時,電感電流一般不能躍變。
這就是動態電路的初始條件。
3)動態電路的初始條件確定方法:
一階電路:可用一階微分方程來進行描述的電路。
零輸入響應:沒有外界電源激勵,僅由儲能元件初始儲能所引起的響應。
在圖示電流、電壓的參考方向下,由KVL得換路后的電路方程:
求得滿足初始條件的微分方程的解,即電容的零輸入響應電壓、電流分別為:
當 t- > ∞ 時,Uc- > 0、i- > 0。
時間常數:一個很重要的概念。觀察零輸入響應表達式,在這里定義:
稱τ為電路的時間常數。它的大小反映了電路過渡過程的進展速度,它是反映過渡過程特征的一個重要的物理量。
時間常數的意義:當 t = τ 時
時間常數就是按照指數規律衰減的量衰減到它的初始值的 36.8% 時所需時間。
理論上:放電要經歷無限大時間才能結束,工程上認為:經過 3τ~5τ 時間過渡過程即告結束。
時間常數越大,衰減越慢,過渡過程持續的時間越長。RC 電路中,電阻 R 在電容 C 放電過程中消耗的全部能量為:
就是說:電容在放電過程中釋放的電場能量全部轉換為電阻消耗的能量(熱能)。
2)RL串聯電路的零輸入響應
圖示電路,原已處于穩態,t = 0 時開關 K 閉合。電流、電壓的參考方向如圖所示,由 KVL 得換路后的電路方程 :
顯然,這是一階常系數線性齊次常微分方程,它的通解為:
從而,求得滿足初始條件的微分方程的解,即電感的零輸入響應電壓、電流分別為
換路后,電感電壓和電流均按指數規律衰減到 0。其曲線如圖所示。RL 電路的時間常數為:
稱 τ 為 RL 電路的時間常數。同樣它的大小反映了電路過渡過程的進展速度。時間常數越大,過渡過程持續的時間越長。
在電路過渡過程中,電感元件不斷放出能量為電阻所消耗,最后,原來儲存在電感中的磁場能量全部被電阻吸收而轉換成熱能。
零狀態:電路中所有儲能元件的初始狀態都為零的情況:
零狀態響應:零狀態電路,由外施激勵所引起的響應。
1)RC 電路的零狀態響應直流電壓源 Us 通過電阻 R 對電容 C 充電,電路如圖所示。在圖示電流、電壓的參考方向下,由 KVL 得換路后的電路方程:
顯然,這是一個一階常系數線性非齊次常微分方程,方程的解有兩部分組成
第一部分為微分方程的特解:稱為強制分量或穩態分量
第二部分為對應齊次方程的通解:稱為自由分量或暫態分量
這個電路方程的通解是
將以下初始條件代入上式得積分常數
最后得到零狀態響應的完全解為:
響應過程:電容電壓 Uc 由零初始值開始以指數形式趨近于它的最終值,即直流電壓源電壓 Us,而電流在換路后瞬間,躍變到最大值,然后以此初始值開始按指數規律衰減到零。
電路接通直流電壓源的過程也就是電源通過電阻對電容充電的過程。在充電過程中,電源輸出的能量一部分轉換成電場能量儲存在電容中,一部分被電阻轉換為熱能消耗。
充電效率問題:
在充電過程中,電源提供的能量只有一半轉換成電場能量儲存于電容中,另一半則為電阻所消耗,也就是說,充電效率為有 50%。
2)RL電路的零狀態響應
和 RC 電路類似,這仍是一個一階常系數線性非齊次常微分方程,解仍由兩部分組成
代入初始條件
電路響應過程:電感電流由零初始值開始以指數形式趨近于它的穩態值,而電壓在換路后,電壓達到最大值,并以此初始值開始按指數規律衰減到零。到達該值后,電壓和電流不再變化,電感相當于短路,其電壓為零,達到新的穩態。
此時,電感的磁場儲能為
注意:直流激勵下的 RC 及 RL 電路的零狀態響應,若外加激勵增加K倍,則其零狀態響應也增加 K 倍,即零狀態響應與外加激勵成線性關系。
附錄
1、電子運動方向
物質是由原子構成,原子又是由原子核和核外電子組成:因原子核(帶正電)質量較大,不易運動;核外電子(帶負電)質量很小(忽略不計),所以在電場力作用下,電子易移動。
電流有正負之分,正電流是電子的空穴在移動,而負電流則是電子在移動。區別就像抽水和壓水造成水管的水流動一樣。
但現在電流方向因前期的誤解形成的俗成是指電子的“空穴”移動方向。所以電子運動方向就是所謂電流方向的反向。
電子的定向移動形成電流,電子移動的方向就是電流的方向。但是為了研究的方便,人們人為設置:正電荷的移動方向是電流的方向。所以電子的移動方向和電流的方向相反。
如上圖,我們規定電流從電源正極流向電源負極,但實際上,由于自由電子帶負電,在電場的作用下,自由電子其實是由電源負極向電源正極運動的。在交流電路中,隨著電壓高低的不同變化,電壓方向的不停變化,自由電子在電路中按照一定的頻率向兩個方向移動。
可能有人會問,直流電有負極,交流電為什么沒有負極?其實,零線就相當于交流電的“負極”。
在交流電路中,隨著電壓方向的不斷變化,自由電子不停流入大地或流出大地,而大地擁有無窮正電荷,也擁有無窮負電荷。所以理論上來說,大地可接收無窮多的電荷,而大地的電位,永遠是“零電位”。就像不管你向大海灑一杯水,還是一盆水,或者X噸水,大海的咸度不會因此而變化。
于高山之巔,方見大河奔涌;于群峰之上,更覺長風浩蕩。覺得不錯,動動發財的小手點個贊哦!
*博客內容為網友個人發布,僅代表博主個人觀點,如有侵權請聯系工作人員刪除。