擾動輸入d(k)到跟蹤誤差e(k)的傳函可表示為

H（z）≡= (1)

式中：N表示一個基波周期的采樣次數。

對應s域中的頻率響應為

H(jω)=H(z) (2)

式中：T代表采樣周期。

如果d(k)的頻率是基波周期的整數倍，并假定Q(z)=1且PB(z)穩定，有

|H(jω)|=0 (3)

這表明重復控制器消除了頻率為基波周期整數倍干擾產生的跟蹤誤差，從而得到了非常好的跟蹤效果。

當然，為了保證系統穩定，一般取Q(z)1，這樣就有

|H(jω)|μ(jω) (4)

式中：μ(jω)為一很小的數。

另外，從直觀上講，重復控制器可以看作N個積分調節器，對應于參考信號的N個采樣點。從而，一個瞬時值跟蹤系統分解為N個恒值調節系統，通過各采樣點的無靜差跟蹤，保證了整個正弦參考信號的跟蹤精度。

重復控制雖然可以保證輸出波形，但它卻有一個致命的弱點。由圖3可以看出，重復控制得到的控制指令并不是立即輸出給系統，而是滯后一個參考周期后才輸出。這樣，如果系統內部出現干擾，消除干擾對輸出的影響至少要一個參考周期。干擾出現后的一個參考周期內，系統對干擾并不產生任何調節作用，這一個周期系統近乎處于開環控制狀態。因此，重復控制系統的動態響應速度是非常慢的。

由于上述原因，對于高要求的光伏系統逆變器不宜單獨采用重復控制[4][5]。采用數字PID控制雖然輸出電壓波形質量不是很高，但它卻是以開關周期對跟蹤誤差進行調節。仔細設計系統參數，可以使系統獲得良好的動態特性。綜合考慮，將兩種控制方式結合在一起，取長補短，利用重復控制改善系統的穩態輸出波形質量，利用數字PID控制或極點配置提高系統的動態特性，使系統兼具良好的穩態和動態特性。

4 實驗結果

針對以上的分析，在一15kW光伏系統單相全橋逆變器上進行了實驗，參數如下:開關器件采用IGBT模塊，濾波電感Lf=0.68mH，濾波電容Cf=50μF，數字信號處理器采用TI公司的TMS320F240DSP，并采用240DSP自帶雙10位A/D轉換器。實驗結果如圖5所示。

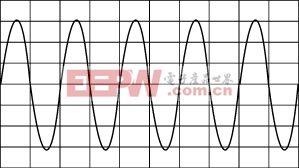
(a) 閉 環 空 載 波 形

(b) 閉 環 加 載 波 形 （R=5Ω）

圖5 實 驗 波 形

從圖5中可以看出，采用離散重復控制可以保證光伏逆變器在空載條件下保持穩定，在帶載條件下可以明顯改善系統的穩態性能，顯著降低系統的穩態誤差。

5 結語

本文分析了光伏發電系統逆變器數字化實現的意義，并對整個系統及其控制電路進行了分析，在控制算法上，采用離散重復控制策略，使系統在周期性擾動信號下的穩態性能得以改善。由于數字化控制的優越性比較明顯，因此在偏遠地區及其它應用場合，數字化光伏發電系統逆變器的應用將會越來越廣泛。