4、無模型控制原理

4.1 無模型控制的總體概述
　　
在控制律設計中一般的需要建立動態系統的數學模型。經典的方法要求這種數學模型必 須事先建立至少其結構必須事先確定。而且模型愈精確愈好。無模型控制律的設計中，突破了控制律對數學模型盡可能事先精確的建立這一要求的限制。
　　
我們的建模手續是伴隨反饋控制而進行的。初始的數學模型可以是不精確的，但必須保證所設計的控制律具有一定的收斂性.我們所設計的無模型控制律是邊建模邊控制，得到新的觀測數據后，再建模再控制.如此繼續下去，使得每次得到的數學模型逐漸精確，從而控制律的性能也隨之得到改善。我們把這種手續稱之為實時建模與反饋控制一體化手續。

4.2 建模與自適應控制一體化途徑

在參考文獻中，提出了如下的泛模型：

y（k）-y（k-1）=φ（k-1）[u（k-1）-u（k-2）> （4-1）

不失一般性，這里假定被控動態系統S的時滯是1,y（k） 是系統S的一維輸出， u（k-1）是P維輸人。φ（k）是特征參量，它是利用某種辨識算法在線估計的，k是離散時間。我們將會看出，在實時辨識D實時反饋校正的辨識與控制一體化手續中，φ（k）有明顯的數學與工程意義。

4.3 實時建模與反饋控制一體化

具體的，我們的建模與反饋控制一體化的框架如下：

（1）依據觀測數據和泛模型

y（k）-y（k-1）=φ（k-1）[u（k-1）-u（k-2）]

利用適當的估值方法，得到了φ（k-1）的估值φ（k-1）。

（2）尋求φ（k-1）的向前一步的預報值φ＊（k），一個簡單的方法就是取

φ＊（k）= φ＊（k-1）

在尋求控制律時，我們把φ＊（k）仍記成社φ（k） 。 （3）把控制律

作用于系統S，得到新的輸出貝y（k+1）。于是得到了一組新的數據｛y（k+1）,u（k）｝ 。

在這組新數據的基礎上重復（1），（2）和（3），即可又得出新的數據｛y（k+2）,u（k+1）｝如此繼續下去。只要系統S滿足一定的條件，在這種手續的作用下，系統s的輸出y（k）將逐漸地逼近y0。

4.4 控制器程序的設計
　　
目前在工業生產過程控制中應用的控制器，絕大多數是經典的PID調節器及其變種，對于耦合情況不嚴重的系統，PID調節器的控制效果還能令人滿意，但對耦合嚴重的系統，PID調節器則顯得無能為力，下面以PID調節器為基準，將無模型控制器與PID調節器進行比較，用于說明無模型控制器具備較好的解耦和抗干擾能力。無模型控制流程圖如下：

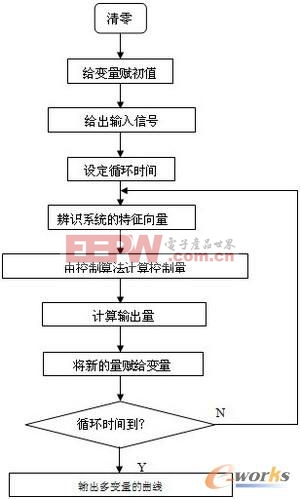
圖3 無模型控制流程圖