基于Alpha-NMF的AD樣本分類及特異性基因選擇方法
1.2 Alpha-NMF算法
Alpha-NMF算法是NMF算法的一種改進,它是針對信號處理所提出的一種新的算法。
Alpha-NMF算法的數學模型為:

2 非負矩陣分解在基因表達譜數據中的應用
2.1 數據預處理
文中所選的實驗數據為基因表達綜合數據庫(GEO)中23組大腦海馬區域(HIP)和23組內嗅區皮質(EC)的AD樣本,54 675個基因表達數據;其中海馬區域的基因數據集由13個control AD樣本和10個affected AD樣本組成,內鼻皮質區域的基因數據集由13個control AD樣本和10個affectedAD樣本組成。由于基因表達譜數據的復雜性,在進行聚類分析前必須先進行預處理和數據轉換等過程。本文先采用小波變換(wave let transform,WT)方法對數據進行降噪,然后通過微陣列顯著性分析(significance analysis of microarrays,SAM)工具箱篩選出顯著變化的上下調基因。
2.2 Alpha-NMF算法應用于基因表達譜數據
Alpha-NMF算法被提出后,至今還設被應用于基因表達數據中,通過大量的實驗,證明了Alpha-NMF算法能夠有效的應用到該領域中,相比傳統NMF算法,其算法穩定性和分類準確率明顯較高。
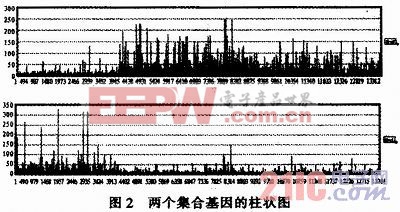
基因表達譜數據的Alpha-NMF混合模型如圖1所示。Y表示mxn維基因表達譜數據,每一行表示一個樣本集,每一列表示一個基因在不同條件下的表達水平。yij表示第j個基因在條件i下的表達水平。通常nm。本文引用地址:http://cqxgywz.com/article/193834.htm

任一樣本yi可以表示為:

也就是說每一個樣本可以近似看做是非負矩陣X的行向量的非負線性組合,組合系數是矩陣A對應行向量的分量。把分解后的矩陣X的每一行稱為一個集合基因。矩陣A的第k列為X的第k個集合基因的系數,若矩陣X能表征原始數據的局部特征,則系數矩陣A與樣本類別緊密相關,即類別c1對于特征k的貢獻大,而c2對于特征k的貢獻小。對于每一個集合基因(圖2為HIP數據經Alpha-NMF算法,α=0.5時分解后相關系數為0.97集合基因的柱狀圖),若元素的值相對較大,說明其對應的基因j與AD緊密相關。
3 實驗結果與分析
首先采用WT-SAM方法分別對HIP和EC數據進行預處理,篩選后的基因數分別為13 587個、6 567個,再對數據進行菲負化處理,然后通過Alphs-NMF算法進行分解,利用分解后的A矩陣進行聚類,本文采用k均值聚類方法對A的行向量進行聚類,得到一聚類結果。對于矩陣X,設定一閾值,篩選出集合基因中大于該閾值的信息基因。







評論