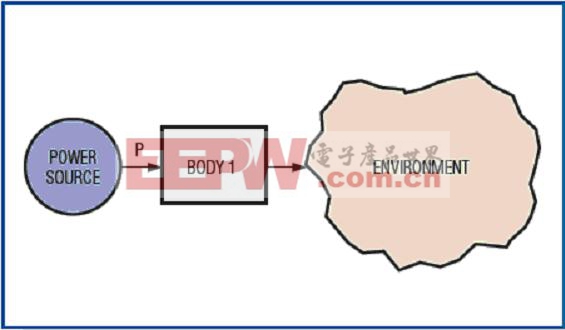
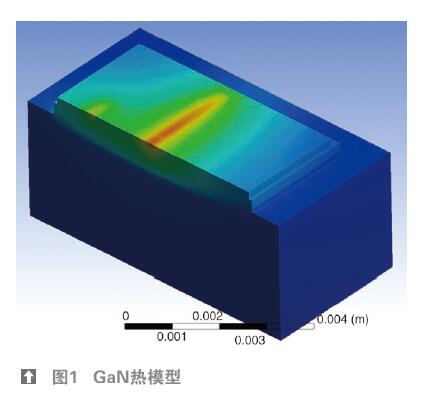
圖2. 該熱模型說明了從外部電源至芯片(組件1)然后再返回到環境的熱流動。

　　已知kA和θJA，即可計算出不同時間的溫度。或者，如果P為時間的復合函數，即可利用以上公式作為時間仿真來評估溫度，并利用MATLAB®軟件編程繪制溫度隨時間變化的函數。θJA由數據資料提供。但是，如果某項配置條件與JEDEC標準規定不同，利用公布的θJA值進行計算會產生誤差。JEDED標準51-3節指出：“值得強調的是，利用這些測試板測試得到的數值不能用于直接預測任何具體應用系統的性能，只能用于封裝之間的比較”2。所以，為了正確估算溫度，應該針對原型開發板測量θJA值，或按照下列說明直接估算。

　　從管芯至環境的熱流動

　　考慮圖3所示的三體系統(與芯片相似)，在管芯處產生熱量并通過環氧樹脂和封裝將熱量耗散至外部環境。組件1為管芯，組件2為環氧樹脂，組件3為芯片封裝。

　　為了求解該系統中的θJA，我們必須為三個物體定義公式。

　　其中：

　　TB1、TB2和TB3分別是組件1、2和3的瞬時溫度；P12是以熱形式從組件1傳導至組件2的功率；P23是以熱形式從組件2傳導至組件3的功率；PG是組件1直接產生的功率，或直接傳導至組件1的功率。管芯產生的功率(PG)減去管芯吸收的功率，得到：

　　從式18、式19和式20求解三體系統比較復雜，但利用拉普拉斯變換可以簡化計算。求解公式為：

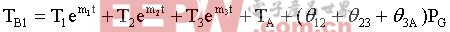(式21)

　　其中：

　　θ12為組件1至組件2的熱阻；θ23為組件2至組件3的熱阻；θ3A為組件3至環境的熱阻；T1、T2和T3為積分常數；m1、m2和m3為k1、k2和k3的函數。

　　管芯產生功耗時，式21能夠以非常準確的方式預測管芯溫度。然而，使用該式時，我們必須知道所有積分常數以及m1、m2和m3，它們為復雜函數，求解非常困難。為了避開這種困難操作，我們利用一個工具求解不同方程：SPICE。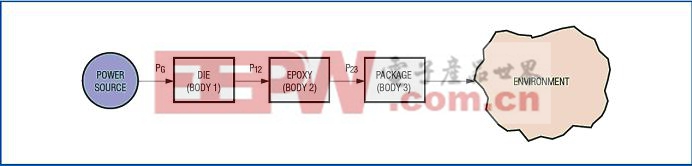

圖3. 三體模型與圖2所示模型的比較。此時，管芯產生的熱流動更為復雜。

　　RC網絡模型瞬態熱特性的微分方程

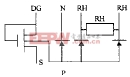
　　現在，我們提出一個類似的微分方程，用作電路建模，我們對電路進行仿真，并通過仿真得到溫度讀數。微分方程18、19和20可通過代表管芯產生功率的RC簡單網絡(圖4)進行模擬。

　　圖4中，電容的初始電壓分別表示管芯(C1)、環氧樹脂(C2)和封裝(C3)的溫度。VA表示環境溫度，IS (流入電容C1的電流)表示管芯產生的功率。表示電容電壓的差分方程為：