由于生產和科學研究迅猛發展，許多最優化問題已無法用古典方法解決，又由于電子計算機日益普及，使最優化問題的研究不僅成為一種迫切需要，而且有了求解的有力工具。現在已經有許多計算機算法解決最優化問題，如Kuhn-Tucker 定理、Be11man 最優化原理和動態規劃、pONTRIAGIN 的極大值原理以及Ka1man 的關于隨機控制系統最優濾波器。

　　最優化節點位于函數選板的“數學→最優化”，如圖所示。

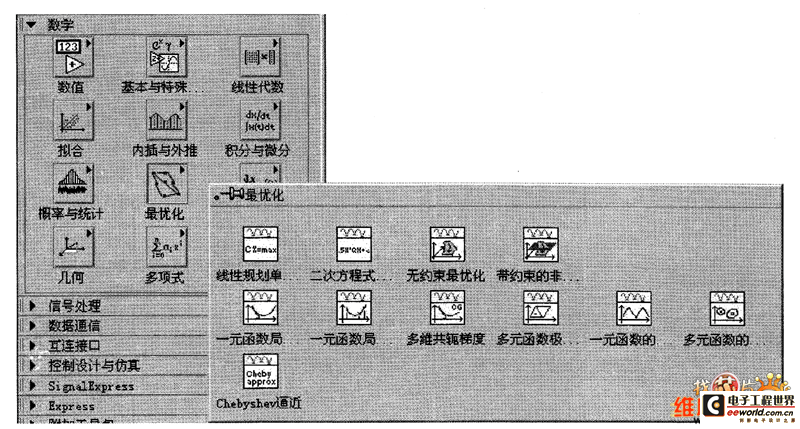
　　如圖 最優化子選板

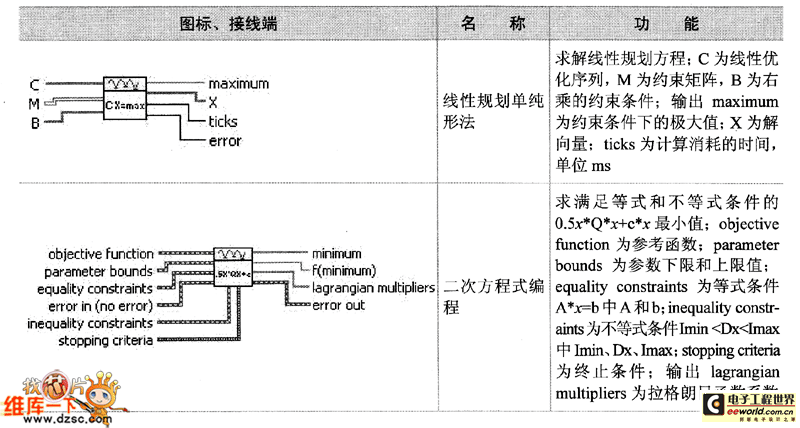
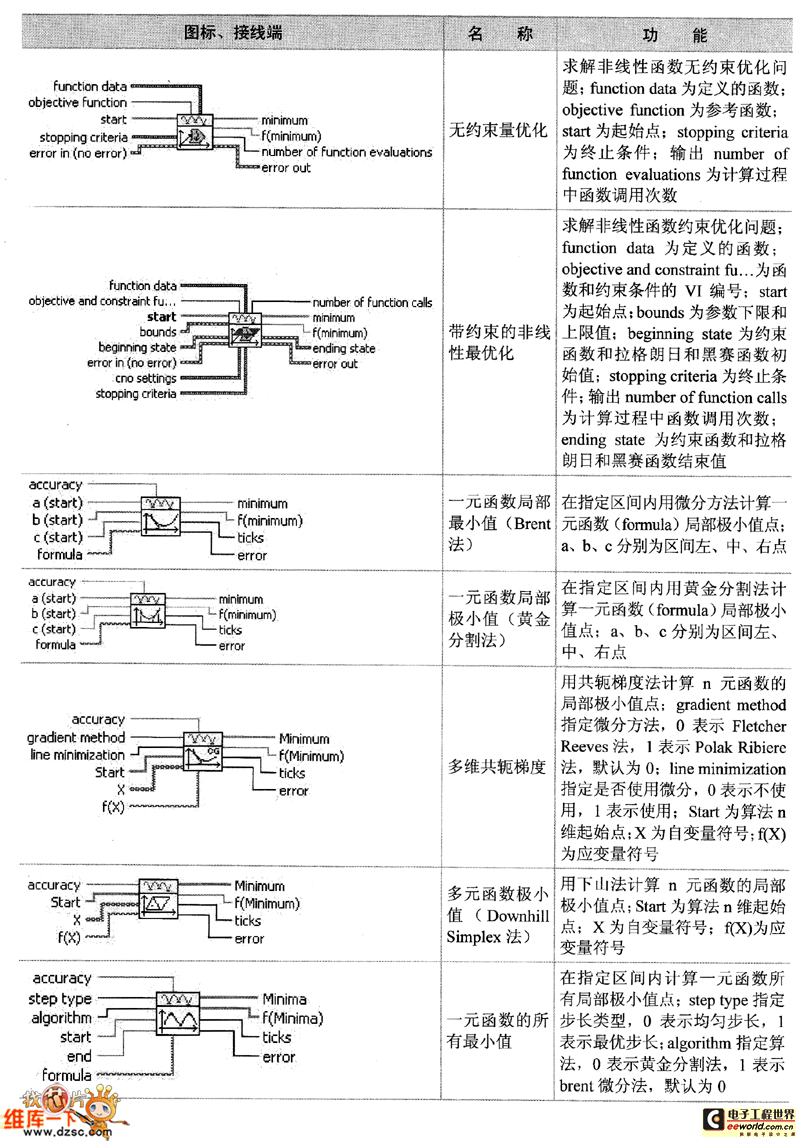
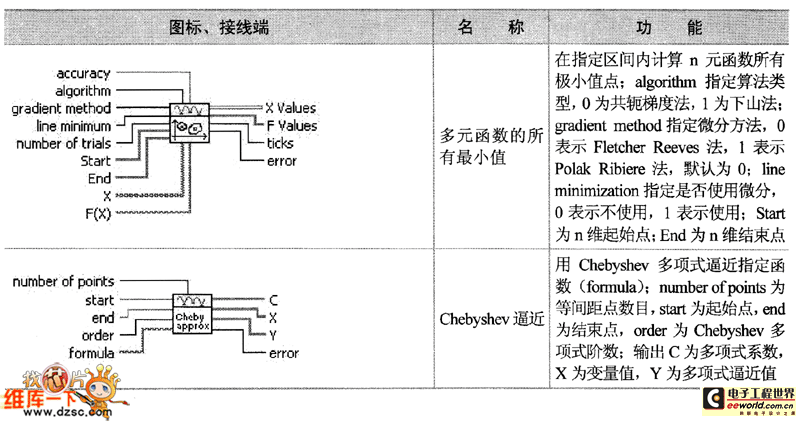
　　如表詳細列出了最優化子選板中函數和Ⅵ節點的圖標、接線端、圖標和功能。其中常見參數說明如下。

　　accuaracy：指定計算的精度，默認為1e-8。

　　mlnlmum：極小值對應的自變量值。

　　f（minimum）：函數極小值。

　　如表 最優化子選板節點