公鑰密碼系統，也稱為非對稱密碼系統，是密碼學的一種形式。它有一對密鑰：公鑰和私鑰。它們在數學上有一定的關系，但是很難從公鑰得到私鑰。公鑰密碼學的兩個主要分支：

公鑰加密：任何人都可以將消息（明文）加密成密文，但只有接收者才能生成有意義的密文。這樣確保了數據的安全性，用于可靠性方面。

數字簽名：發送者通過私鑰加密的消息(明文)，可以被任何人通過公鑰解密。因此證明了這條消息是發送者簽名并且沒被人修改過。這種方法用于數字簽名與認證方面。

公鑰制密碼學中，目前應用最為廣泛的是RSA公鑰制密碼算法[1]。RSA算法通過模冪運算實現，模冪運算是整個RSA算法的核心。在操作數較小的情況下，模冪運算比較簡單，可以直接計算。但是為了保證必要的安全等級，一般采用512 bit或1 024 bit的密鑰長度，在銀行等需要更高安全等級的系統中，會采用更長位寬的密鑰，模冪的難度隨之成指數級增長。RSA算法安全性的保證和需要就像一把雙刃劍，在給攻擊者帶來計算難度的同時也提高了運算的復雜度。

本文提出一種基于ASIC設計的高速、可配置的RSA密碼協處理器體系結構，可實現256 bit到2 048 bit的RSA加密運算。該方案綜合考慮RSA模冪和模乘算法的特點和瓶頸，采用改進的高基模乘算法和流水線結構，提高運算速度；采用DMA直接訪問方式，消除協處理器與內存之間的通信速度瓶頸；數據輸入輸出都使用雙口存儲體，形成加解密數據流。

1 公鑰密碼算法RSA

1.1 RSA算法

RSA加密算法是目前在理論和實際應用中較為成功的公鑰密碼體制，它的安全性是基于數論中大整數分解為素數因子的困難性，這一困難在目前仍是一個NP問題。要建立一個RSA密碼系統，首先任選兩個大素數p、q，使：

N=p×q

并得到Euler函數:

Ψ(n)=(p-1)×(q-1)

然后任選一個與Ψ(n)互素的整數e作為密鑰，再根據e求出解密密鑰d，d滿足：

d×e=1modΨ(n)

事實上，加密密鑰e和解密密鑰d是完全可互換的，因此在求e或d時，不論先假設哪一個，再由它去求另一個都是一樣的。對某個明文分組M和密文分組C，加密和解密的過程如下：

加密過程：

C=MemodN

而解密過程是：

M=CdmodN

RSA加解密就是做模冪運算的過程，而模冪運算是通過一系列的模乘運算得到的。模冪算法根據冪指數掃描順序不同可以分為兩種：從左往右的L-R算法和從右往左的R-L算法。

算法一：R-L模冪算法

式中n為指數e的位數，P為中間變量

輸入：M，e，N；

輸出：C=Me modN；

(1)P=M；C=1；

(2)for i=0 to n-2；

(3)if e[i]=1 then C=C×P mod N；

(4)P=P×P mod N；

(5)next i；

(6)if e[n-1]=1 then C=C×P mod N；

(7)return C；

算法二：L-R模冪算法

輸入：M，e，N；

輸出：C=Me modN；

(1)if e[n-1]=1 then C=M，else C=1；

(2)for i=n-2 to 1；

(3)C=C×C mod N；

(4)if e[i]=1 then C=C×M mod N；

(5)next i；

(6)return C；

從以上兩種算法可以看出，一次模冪運算需要進行N次平方模運算和平均N/2次乘法模運算；但在從右往左的掃描中，乘法和平方是相互獨立的，可以并行。因此可以增加一個N位的乘法器，一個做乘法，一個做平方，這可以顯著提高一次模冪運算的速度。本文面向高速應用場合，因此采用R-L模冪算法。

在RSA算法中，不論是加密過程還是解密過程，都有一個共同的模乘運算(ABmod N)，這個看似簡單的運算，需要做一次乘法和一次除法，最后取余數。但由于M，e，C，d，N等參數的長度通常是1 024個二進制位或更高，使得模冪運算量巨大，很難在一般的協處理器上或處理器上運行，直到1985年由Montgomery提出了一種免除法的模乘算法[2]，才使RSA算法在硬件和軟件中得以實現。

1.2 Montgomery模乘算法

Montgomery算法的基本思想是把一個大整數轉換為一個模R(R通常取2r)的余數表示形式，用轉換后的余數進行一系列模乘運算，最后再轉換為正常的表達形式。將計算A*B mod N時的mod N的除法運算轉化為簡單的移位運算，能夠有效地提高模乘運算的速度。

算法三：Montgomery算法

設N為模數，R是2的整數冪，且R>N，并令R-1和N′滿足0-1-1-NN′=1成立。

輸入：A，B，R，N；

輸出：c=M(A，B)=A*B*R-1 modN

(1)T=A*B；

(2)m=(Tmod R)*N′ mod R；

(3)c=(T+mN)/R；

(4)if c>=N return c-N；

(5)else return m；

該算法不能直接實現RSA算法，需要進行相應的預處理才能消除R-1帶來的影響（見算法五）。該算法仍然包含大整數的乘法，因此需要對其進行改進，使用高基模乘算法（見算法四），細化為小整數的乘法，以便于硬件實現。另外，該算法最后需要判斷m是否大于N，如果大于N，必須再做減法，這在硬件設計上會增加額外的芯片面積。本文通過在模乘循環過程中增加一次循環，就可以免去最后的減法（見算法五）。

1.3 高基Montgomery算法

把n位大整數A，B，N分別表示成s位r進制整數，即A=(as-1 as-2…a0)，B=(bs-1bs-2…b0)r，N=(ns-1ns-2…n0)r，且R=rs，s=n/r，則有N P>

算法四：高基Montgomery算法

Function M(A，B)

S：=0；m=0；

(1)計算中間結果m[i]：

for i=0 to s-1

{for j=0 to i

{s：=s+a[j]*b[i-j]+m[j]*n[i-j]；}

m[i]：=s*n′[i] mod r；

s：=s+m[i]n[i]

s：=s/r；}

(2)計算最終結果并存于m[i]中：

for i=s to 2s-1

{for j=i-s+1 to s-1

{s=s+a[j]b[I-j]+m[j]n[I-j]}

m[i-s]：=s mod r

s：=s/r}

算法五：從右往左掃描的免減高基模乘算法

(1)預處理：

R2=R*R mod N；(事先計算出來，可消除R-1帶來的影響)

P=M（M，R2）；

C=1；

(2)中處理：

for i=0 to n-2

if e[i]=1 then C=M(C，P)；

P=M(P，P)；

next i；

if e[n-1]=1 then C=M(C，P)；

return C；（計算C=M(Me))

(3)后處理：

C=M（C，1）；（免去了montgomery算法每次的減法運算）。

2 協處理器體系結構

2.1 SPU整體結構與模塊劃分

SPU與CPU通過CROSSBAR[3]交叉通信開關進行通信，而SPU與MEM之間則采取DMA方式直接通信，這樣可以消除數據存取的速度瓶頸。同時，當SPU進行加解密工作時，CPU可以并行執行其他指令(只要不發生數據相關)。

SPU劃分為控制模塊，數據通道和存儲單元。其中控制單元主要用于密鑰移位控制，控制密鑰的降冪，并根據密鑰產生乘或平方控制信號。另外，控制單元還包括一個狀態控制器，用于對前處理、中處理和后處理各個運算環節的控制。

數據通道部分則由Montgomery模乘單元和平方單元構成，兩個單元并行，根據控制單元產生的控制信號來進行相應的操作，產生部分積和中間結果。

存儲單元大小為8 Kbit，分為兩部分。一部分是4 KB的RAM，用于加解密過程中暫存數據，以便形成流水線；另一部分是4 KB的ROM，用于存放公鑰和密鑰，掉電可以保存數據。

系統框圖如圖1所示。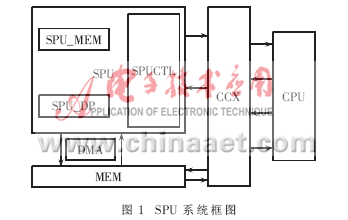

2.2 流水線設計

為了實現高速、可配置的RSA密碼協處理器，采用了按字讀入的高基模乘算法，同時對模冪單元采用流水線結構：這樣一方面可以增加數據吞吐率，加快數據運算速度；另一方面可以通過增減流水線的級數來增強可配置性。

從按字讀入的高基模乘算法（算法五）中可以看出，每次密鑰長度為N bit的RSA加解密過程是一次冪指數為N的模冪運算，而一次這樣的模冪運算則是N次模乘運算。因此通過設計模冪流水線結構，可以大大增加RSA加解密的速度。

流水線結構的模冪運算如圖2所示。明文M經過T級流水線數據通路，最后輸出密文C；對于一個N位的RSA加密系統來說，如果采用T級流水線，則每一級流水線需要循環做N/T次MM運算。RSA的運算速度取決于一級流水線的速度。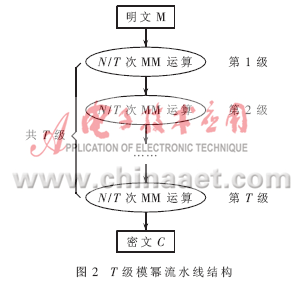

2.3 DMA通道的工作過程

SPU向DMA控制器發出DMA請求，DMA控制器在接到SPU發出的DMA請求后，向CPU發出總線請求，請求CPU脫離對總線的控制，而由DMA控制器接管對系統總線的控制；CPU在執行完當前指令的當前總線周期后，向DMA控制器發出總線響應信號，CPU脫離對系統總線的控制，處于等待狀態(但一直監視DMAC)；DMA控制器接管對系統總線的控制；DMA控制器向SPU發出DMA應答信號，DMA控制器把存儲器與SPU之間進行數據傳送所需要的有關地址送到總線，通過控制總線向存儲器和SPU發出讀或寫信號，從而完成一個字節的傳送；當設定的字節數據傳送完畢后(DMA控制器自動計數)，DMA控制器將總線請求信號變成無效，同時脫離對總線的控制；CPU檢測到總線請求信號變成無效后(CPU一直監視著)，也將總線響應信號變成無效，CPU恢復對系統總線的控制，繼續執行被DMA控制器中斷的當前指令的當前總線周期。

2.4 存儲體結構設計

SPU內部共設計兩部分RAM，都使用雙口存儲體，主要用作數據輸入、輸出緩存。雙口RAM分A和B兩部分，每部分的深度32，寬度64，即32×64的存儲空間；一塊RAM可以存儲2 KB的數據，輸入輸出各需要一塊作為緩存，也就是說片內共設計4 KB的RAM。雙口RAM的兩部分是對稱的，但是對每部分的讀寫都是獨立的，當需要加密或解密時，數據先輸入到A部分，當A部分輸入滿2 KB數據時，數據繼續輸入到B中，此時運算模塊讀取A中的數據計算，當B部分數據輸入滿時，運算模塊已經計算完A中的數據，然后讀取B中的數據，輸出則是相反的過程，如此形成加解密數據流，運算流程如圖3所示。

本文基于改進的按字輸入的從右往左掃描的高基Montgomery模乘算法，提出了一種高速、可配置的RSA加解密協處理器的ASIC設計方案。該方案很好地解決了模冪和模乘運算的瓶頸問題，提高了算法并行性和運算效率。基于該方案可以方便地設計出各種速度和密鑰長度的RSA密碼協處理器，尤其對高速RSA市場具有很廣闊的應用前景。