單邊帶（SSB）調制通過抑制上邊帶或下邊帶來提高帶寬利用率。本文將解析無需使用銳截止濾波器即可實現該技術的電路原理與數學基礎。 

1915年，約翰·倫肖·卡森提交了美國首個單邊帶調制專利申請。他提出的濾波法通過對雙邊帶（DSB）信號進行濾波來消除其中一個邊帶。但由于DSB信號上下邊帶間隔極小，這種方法需要極其陡峭的濾波器。 

1924年，卡森的同事拉爾夫·V·L·哈特利提出了第二種方案——相位法，通過改進電路結構而非依賴輸出端帶通濾波器來消除目標邊帶。該方法無需使用高選擇性帶通濾波器。 

本文將深入探討相位法，并闡釋希爾伯特變換的關鍵作用。這種在信號處理中廣泛應用的數學工具，能對輸入信號的各頻率分量施加寬帶90度相移，是實現相位法的核心所在。 

雙邊帶調制回顧 

以單頻輸入信號為例，設基帶信號為： 

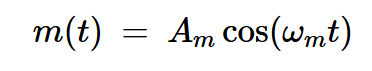
公式1

其頻譜由±fm處的兩個沖激組成： 

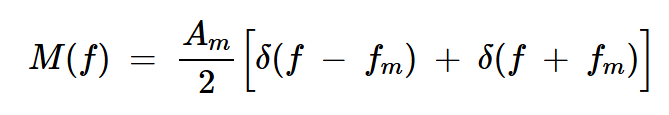
公式2

采用抑制載波的雙邊帶（DSB-SC）調制時，載波信號

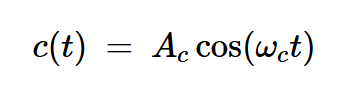
公式3

與基帶信號相乘后產生： 

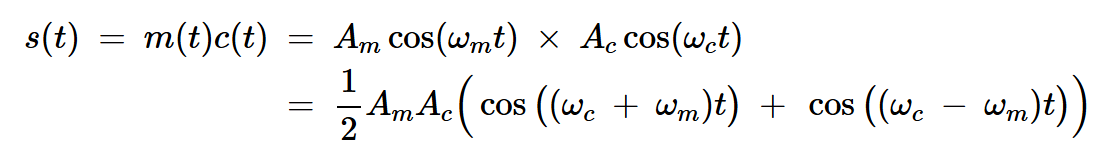
公式4

圖1展示了單頻輸入時的DSB-SC信號頻譜，其中USB和LSB分別表示上下邊帶。 

相位法基本原理

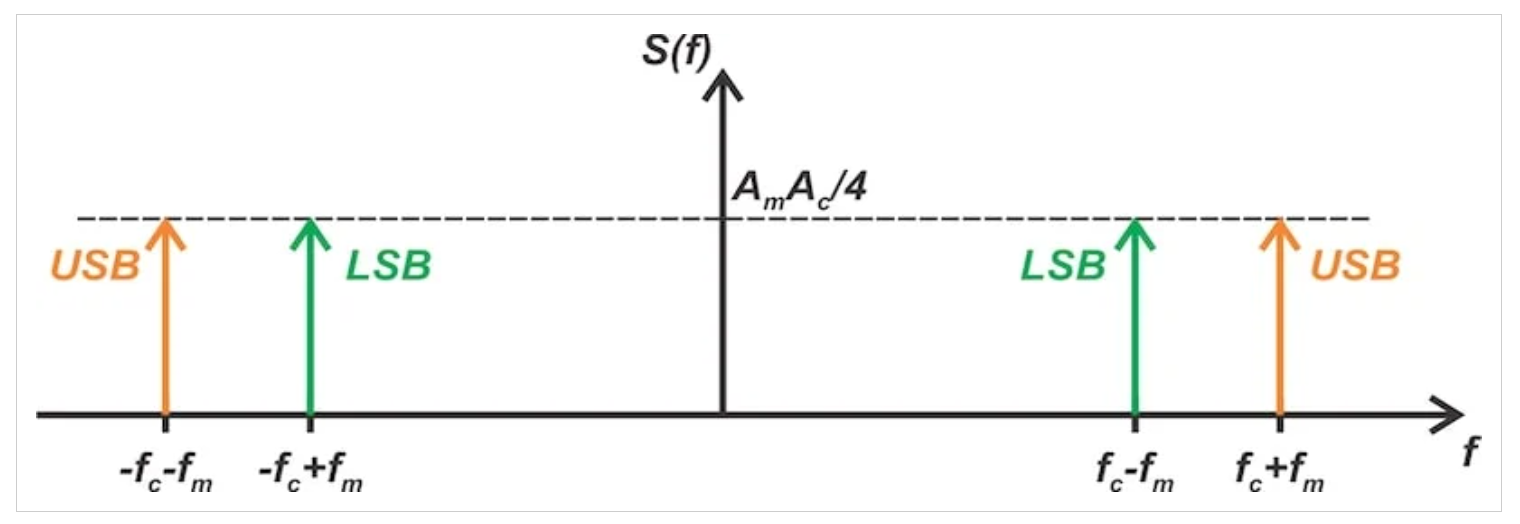
圖1 

SSB調制的核心在于僅保留和頻（USB）或差頻（LSB）分量。根據三角恒等式展開： 

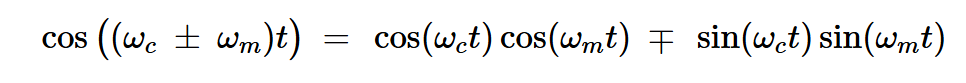
公式5

要實現該式，需從m(t) = cos(ωmt)生成sin(ωmt)。

由于

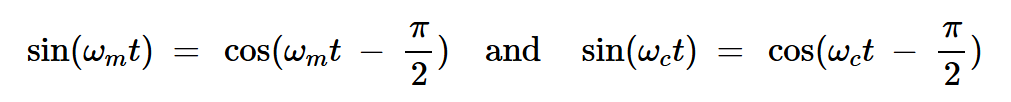
公式6

因此需要精確的-90度移相網絡。

圖2展示了基于該原理的SSB調制器框圖，通過選擇加法器或減法器可分別生成下邊帶或上邊帶。

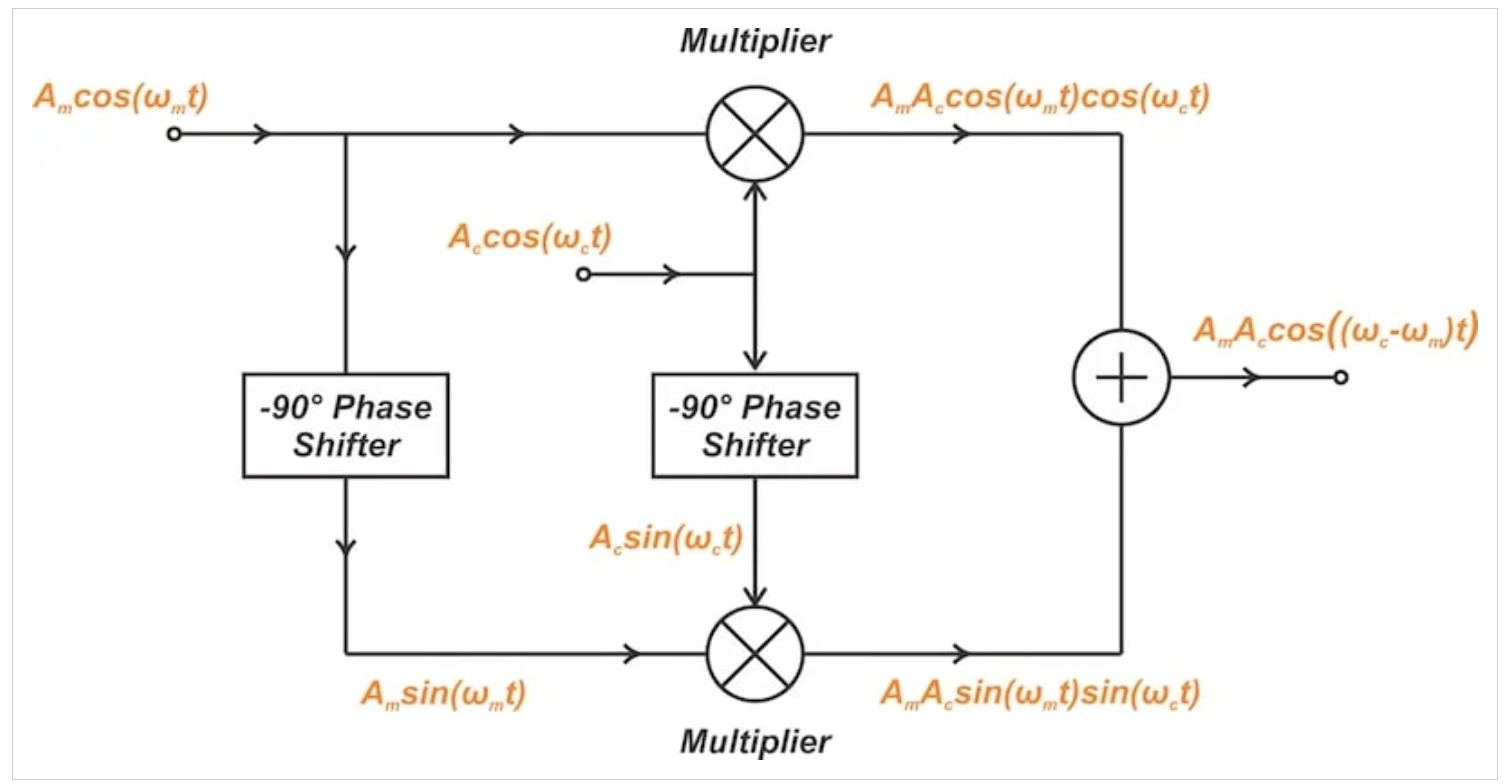
圖2 

 希爾伯特變換 

希爾伯特變換得名于德國杰出數學家大衛·希爾伯特，其開創性工作對數學發展產生了深遠影響。他不僅創立了希爾伯特空間理論，更為泛函分析奠定了重要基礎。 

該變換將所有正頻率分量相移-90度，負頻率分量相移+90度，同時保持頻譜幅值不變。從頻域看，希爾伯特變換相當于一個具有如下響應的線性濾波器： 

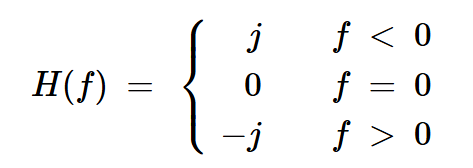
公式7

圖3展示了該變換的幅頻與相頻特性。 

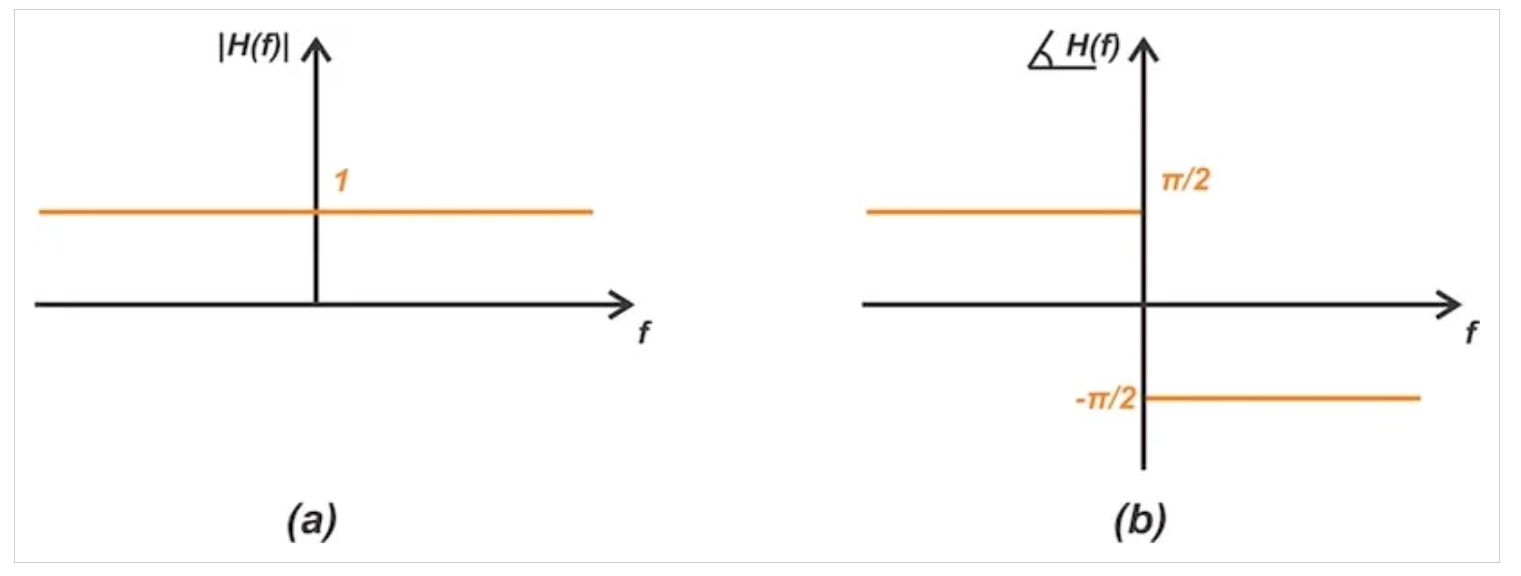
圖3

時域中的希爾伯特變換 

其沖激響應為： 

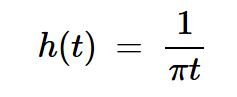
公式8

 余弦/正弦函數的變換驗證 

雖然希爾伯特變換對正負頻率分量的差異化處理看似復雜，但通過歐拉公式可直觀驗證其對余弦函數的變換效果。對于實余弦信號： 

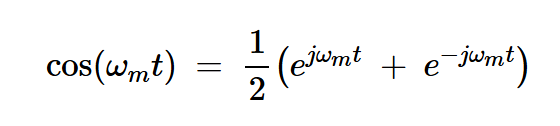
公式9

方程右側的第一項表示正頻率。它經歷了 –90 度的相移。第二項對應于負頻率，并在相位上偏移 +90 度。cos（?mt） 和 sin（?mt） 的計算方法如下： 

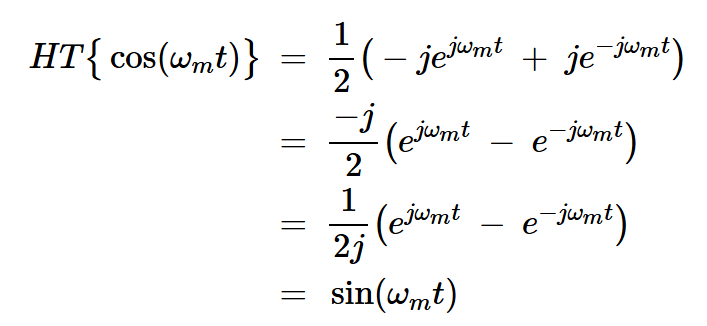
公式10

同理可證： 

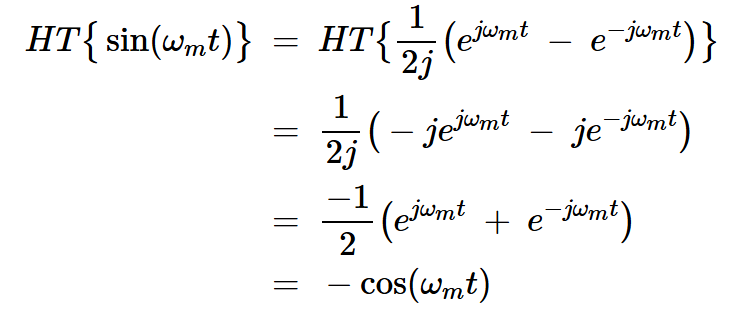
公式11

這一特性表明：若  mh(t)是(?mt)的希爾伯特變換，則對 mh(t) 再次變換將得到 -mh(t) 。 

 在SSB調制中的應用 

圖4展示了相位法的完整實現架構： 

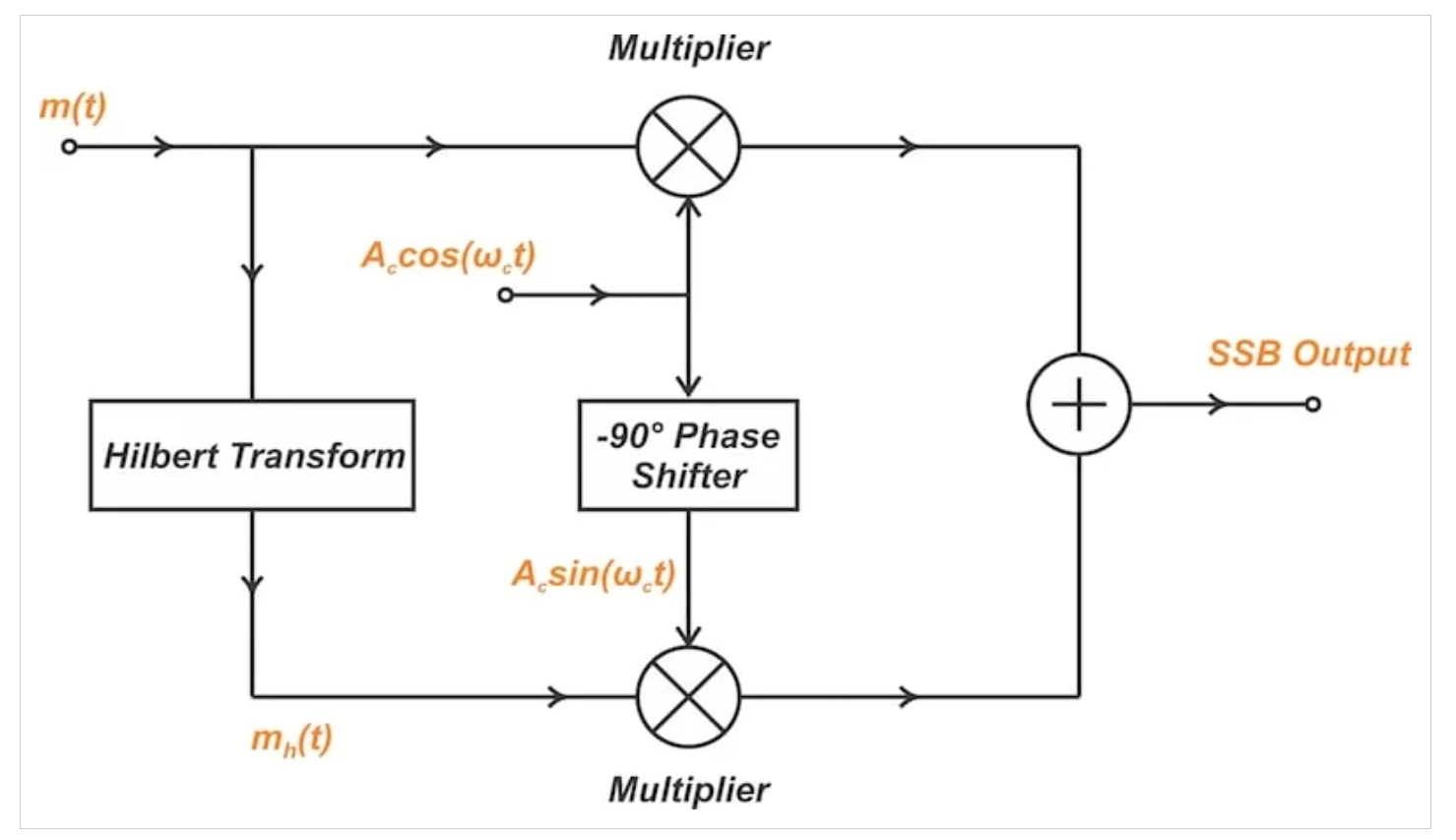
圖4

1. 主通路：基帶信號$m(t)$與載波直接調制 

2. 正交通路：$m(t)$與載波分別經希爾伯特變換后調制 

兩路信號合成時，相位差導致目標邊帶相消。實際系統中： 

- 移相網絡采用無源電路或數字信號處理實現 

- 乘法器多使用平衡調制器結構 

- 載波抑制度取決于調制器平衡精度 

- 邊帶抑制效果由移相模塊決定 

SSB信號的時域表達式為： 

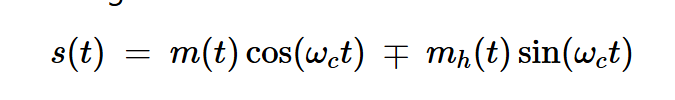
公式12

其中mh(t） 為 m（t）的希爾伯特變換，"+"生成下邊帶，"-"生成上邊帶（假設載波幅度c= 1 。 

總結 

相位法首先生成小功率SSB信號，再通過線性射頻放大器提升至發射功率。該方法的優勢在于通過精確相位控制實現邊帶選擇，避免了傳統濾波法對陡峭濾波器的依賴。后續將通過圖解方式進一步解析其工作原理。 

（注：所有數學符號保留原格式，關鍵術語如"平衡調制器"等采用通信領域標準譯法，公式編號與原文保持一致。）