頻率響應法--奈奎斯特穩定判據 前面我們從代數角度出發討論了控制系統穩定性的定義和勞斯-赫爾維茨穩定判據。本節介紹判別系統穩定性的另一種判據――奈奎斯特穩定判據。該判據是根據開環頻率特性來判定閉環系統的穩定性。同時,它還能反映系統的相對穩定的程度,對于不穩定的系統,判據與勞斯穩定判據一樣,還能確切回答閉環系統有多少個不穩定的特征根。 對于圖5-34所示的反饋控制系統,閉環傳遞函數為:
其特征方程式為 令 將式(5-40)代入式(5-39)得 式中, 、 、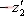 、…、 、…、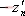 是 是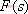 的零點,也是閉環特征方程式的根; 的零點,也是閉環特征方程式的根; 、 、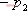 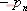 、…、 是 、…、 是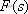 的極點,也是開環傳遞函數的極點。因此根據前述閉環系統穩定的充分必要條件,要使閉環系統穩定,特征函數 的極點,也是開環傳遞函數的極點。因此根據前述閉環系統穩定的充分必要條件,要使閉環系統穩定,特征函數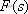 的全部零點都必須位于s平面的左半平面上。 的全部零點都必須位于s平面的左半平面上。 5.4.1 輻角原理 由于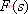 是s的有理分式,則由復變函數的理論知道, 是s的有理分式,則由復變函數的理論知道,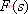 除了在s平面上的有限個奇點外,它總是解析的,即為單值、連續的正則函數。因而對于s平面上的每一點,在 除了在s平面上的有限個奇點外,它總是解析的,即為單值、連續的正則函數。因而對于s平面上的每一點,在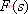 平面上必有唯一的一個映射點與之相對應。同理,對s平面上任意一條不通過 平面上必有唯一的一個映射點與之相對應。同理,對s平面上任意一條不通過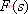 的極點和零點的閉合曲線 的極點和零點的閉合曲線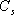 ,在 ,在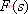 平面上必有唯一的一條閉合曲線 平面上必有唯一的一條閉合曲線 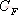 與之相對應,如圖5-35所示。若s平面上的閉合曲線 與之相對應,如圖5-35所示。若s平面上的閉合曲線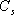 按順時針方向運動,則其在 按順時針方向運動,則其在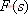 平面上的映射曲線 平面上的映射曲線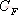 的運動方向可能是順時針,也可能是逆時針,它完全取決于復變函數 的運動方向可能是順時針,也可能是逆時針,它完全取決于復變函數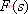 本身的特性。在此我們感興趣的不是映射曲線 本身的特性。在此我們感興趣的不是映射曲線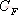 的具體形狀,而是它是否包圍 的具體形狀,而是它是否包圍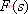 平面的坐標原點以及圍繞原點的方向和圈數,因為它與系統的穩定性有著密切的關系。 平面的坐標原點以及圍繞原點的方向和圈數,因為它與系統的穩定性有著密切的關系。 | 圖5-35 s平面上封閉曲線及其在F(s)平面上的映射線 |
圖5-35 s平面上封閉曲線及其在F(s)平面上的映射線 由式(5-41)可知,復變函數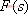 的相角為 的相角為 假設s平面上的閉合曲線

技術專區
|
|
評論