頻率響應法--奈奎斯特穩定判據
加入技術交流群
曲線以順時針方向包圍（-1，j0）點旋轉兩周，這意味著有兩個閉環極點位于s右半平面上，該閉環系統是不穩定的。 |
2、利用奈氏判據確定系統的參數穩定范圍
如果系統中的某個參數或若干個參數是可以變化的，為使系統穩定，可利用奈氏判據來確定系統的參數穩定范圍，即根據奈氏曲線是否通過（－1，j0）點的條件來選定參數。下面以例說明之。
例5－8 試用奈氏判據確定該閉環系統穩定的K值范圍。
已知一單位反饋系統的開環傳遞函數為
 |
試用奈氏判據確定該閉環系統穩定的K值范圍。
解 該系統是一個非最相位系統，其開環系統幅頻和相頻特性的表達式分別為
 |
 |
 |
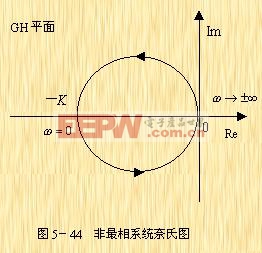和慣性環節一樣，它的奈氏圖也是一個圓，如圖5－44所示。由于系統的P＝1，當ω由
變化時，
曲線如按逆時針方向圍繞（－1，j0）點旋轉一周，即N＝－1，則Z＝1－1＝0，表示閉環系統是穩定的。由圖5－44可見，系統穩定的條件是K＞1。
3、具有時滯環節的穩定性分析
由于時滯系統的開環傳遞函數中有著
的環節，其閉環特征方程為一超越方程，因而勞斯穩定判據就不適用了。但是，奈氏穩定判據卻能較方便地用于對這類系統穩定性的判別。
設含有時滯環節的開環系統的傳遞如下：
 |
|
式中， 
為時滯時間常數。將上式改寫成：
 |
|
其中
 |
|
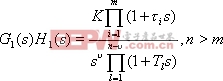不含時滯環節的傳遞函數。相應地，開環系統的幅頻特性和相頻特性為：
 |
|
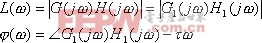上式表明，當
時，相對于
，
的幅值沒有變化，而相角則在每個
上順時針多轉動了
。
由于實際的控制系統中，
，因此當
時，
的模趨于零，因而
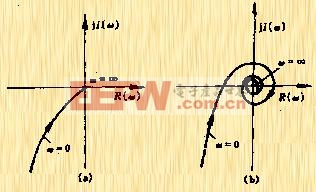
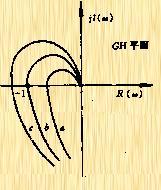
隨
以螺旋形趨于原點，并且與GH平面的負半軸相交無窮點，如圖5－45。因此為使系統穩定，奈氏曲線與負實軸相交點必須位于（－1，j0）的左邊。
 |
| 圖5-45 |
例5－9 試分析滯后時間 對系統穩定性的影響。
設一時滯控制系統如圖5－46所示。已知圖中的 
，試分析滯后時間
對系統穩定性的影響。
 |
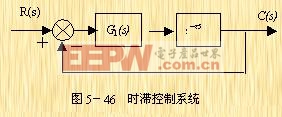解 系統的開環傳遞函數為
 |
|
取
值分別為0,2，4，圖5－47示出了式（5－51）在不同 
值時的奈氏曲線。由圖可見，當滯后時間
為零時，系統相當于無時滯環節，
不包圍（－1，j0）,所以閉環
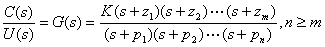
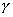
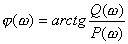
評論