摘要：提出一種基于鄰域匹配度和能量加權平均的多源遙感圖像曲波變換融合方法。對低分辨率的多光譜圖像和高分辨率的全色圖像作曲波變換，融合圖像的曲渡系數中的低頻分量取自多光譜圖像的低頻分量。求兩幅圖像高頻系數鄰域內的匹配度，與閾值相比較，根據比較結果分別采用不同方法確定高頻系數。對生成系數進行逆曲波變換后得到融合圖像。實驗表明融合后的圖像清晰度和光譜性得到有效提高。

關鍵詞：圖像融合；曲波變換；鄰域能量；匹配度

曲波變換能夠有效地描述具有曲線或超平面奇異性的高維信號。對一幅圖像進行N尺度曲波變換后，第一層是低頻系數，表示圖像的輪廓信息；第N層是高頻系數，體現圖像的細節和邊緣特征。2～N-1層是中高頻系數層，包含著圖像元素的邊緣特征，具備多方向性。遙感圖像的曲波變換融合一般采取基于像素的融合規則：粗尺度系數采用多光譜圖像的粗尺度系數，細尺度系數采用多光譜圖像和全色圖象變換系數模值較大的細尺度系數。在設計融合規則時要基于鄰域，考察鄰域內的統計特性，可有效提高融合質量。

1 基于曲波變換的融合方法

Curvelet繼承和發展了小波分析優良的空域和頻域局部特性，是一個新的多尺度變換分析工具，其相對于小波的優勢在于更加適合描述圖像的幾何特征，更適合提取圖像的細節信息。這是因為小波采用的是“塊基”(block base)，在逼近邊緣時常常會產生環繞現象，模糊了邊緣：而curvelet采用的是“楔形基”逼近，與小波最大的差異就是具有任意角度的方向性，不像小波只具有水平、垂直、對角線3個方向，所以是各向異性的。在楔形分塊中，只有當逼近基與奇異性特征重疊，即其方向與奇異性特征的幾何形狀匹配時，才具有較大的curvelet系數。此外，curvelet較之小波具有更好的稀疏表達能力，它能將圖像的邊緣，如曲線、直線特征用較少的大的curvelet變換系數表示，克服了小波變換中傳播重要特征到多個尺度上的缺點，變換后能量更加集中，更利于跟蹤和分析圖像的重要特征。因此，將curvelet變換引入圖像融合，可以利用eurvelet分析更好地提取原始圖像的特征，為融合圖像提供更多的信息。

融合的基本步驟為：

1)對源圖像分別進行曲波變換，得到不同分辨率層次下的曲波系數，包括coarse層、detail層和fine層；

2)根據融合應用目的的不同，對不同尺度層采用不同的融合規則進行處理。針對遙感圖像的曲波變換融合一般采取的融合規則為：粗尺度系數采用多光譜圖像的粗尺度系數，細尺度系數采用模值絕對值大的細尺度系數；

3)對融合的各層曲波系數進行曲波逆變換得到融合圖像。

融合流程如圖1所示。

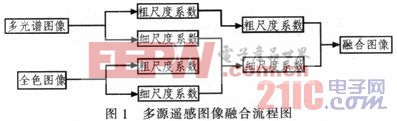
步驟2中融合方式是基于單像素的融合方式。多源遙感圖像不同波段的多光譜圖像成像方式不同，光譜特征差別大，相關性差，精確配準難度高。基于單像素的融合方式沒有考慮區域信息，不適宜應用在具備上述特征的多源遙感圖像之間的融合，所以在設計融合規則時要基于鄰域，考慮區域的統計特性和匹配程度，根據鄰域的匹配程度分類高頻系數的提取方式，用兩幅圖像的鄰域統計特性確定加權系數。

2 基于鄰域能量和匹配度融合規則設計

區域的統計特性主要有能量、方差和梯度等，能量用曲波系數的平方表示，曲波變換后能量主要集中在低頻系數上，高頻系數的能量隨變換層數遞減。匹配度表征了不同圖像區域的相關程度。文獻中直接對像素灰度在鄰域內按照匹配度大小進行能量的加權處理，融合得到的圖像作為二次融合的圖像源。文中將曲波變換引入上述過程，在曲波變換域中考慮鄰域的匹配度，根據鄰域的匹配程度分別采用不同的高頻系數提取方式，在加權處理中用兩幅圖像的鄰域能量確定加權系數。

V(x，y)表示系數矩陣中點(x，y)的值；下標k=M、H or F，M表示多光譜圖像，H表示高分辨率圖像，F表示融合后圖像。在多光譜圖像和高分辨率圖像曲波變換高頻系數矩陣的鄰域內定義匹配度：

高分辨率全色圖像和低分辨率多光譜圖像進行曲波變換融合時，根據匹配度的大小對中心點進行系數值的選取。如果匹配度小于閾值λ，說明兩幅圖像在該位置空間特性差異較大，因此選擇能量較大區域的中心像素為融合圖像的像素；如果匹配度大于閾值λ，說明兩幅圖像有較強的相關性，則進行加權處理。鄰域能量較小的高頻系數對應的權值：

Kmin=0．5-0．5(1-MC)／(1-λ)

鄰域能量較大的高頻系數對應的權值：

Kmax=1-Kmin

高頻系數的選取規則為：

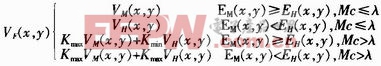
曲波變換融合中，基于鄰域能量和匹配度融合規則設計如下：

1)coarse層即低頻系數采用多光譜圖像的粗尺度系數；

2)detail層和fine層．即中高頻和高頻分量采用上述高頻系數的選取規則。