可求出反射到照明面上的光束R 的照度為：

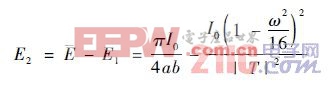
　　2. 3 偏微分方程

　　該反射過程中，入射光I 的強度I 與反射光R照到t 點的照度E2滿足偏微分方程：

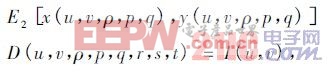
　　其中：

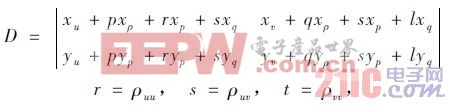
x 和y 由2. 1 中的結果給出。入射到反射面上的光線I 的強度：

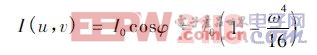
　　E2由2. 2 中的結果給出。將以上結果帶入偏微分方程，列出偏微分方程的具體形式。

　　偏微分方程的邊界條件由朗伯型光源的發光特性和矩形均勻照明區域決定。首先設置反射面的下邊緣也為一個長寬比例為a∶ b 的矩形，讓直接照射到照明面上的光為一個矩形光斑。而朗伯型LED 光源的發光角度為120°，因此反射面的上邊緣在一個頂角為120°的圓錐面上。用數值求解法將上式進行離散化，計算偏微分方程。設置反射面的下邊緣初始點坐標作為初始點條件，結合邊界條件，帶入計算機程序迭代計算方程，求出反射面上一系列的點的坐標。

　　3 模擬與仿真

　　將求解出的反射面的一系列點輸入建模軟件ProE 中，擬合成一個實體反射面，如圖4 所示。再將該反射面導入光學仿真軟件Tracepro 中，模擬驗證最終的效果，得到照明面上的照度分布圖，如圖5 所示。在中間照明區域，光照的均勻度可達85% 以上，能實現比較理想的照明效果。因為在建模過程中，是先輸入點，形成樣條曲線，再由樣條曲線形成最終的反射面，這個過程中采用了平滑的算法，引入了誤差，使最后結果有點失真，但失真程度不大。

圖4 反射面結構圖

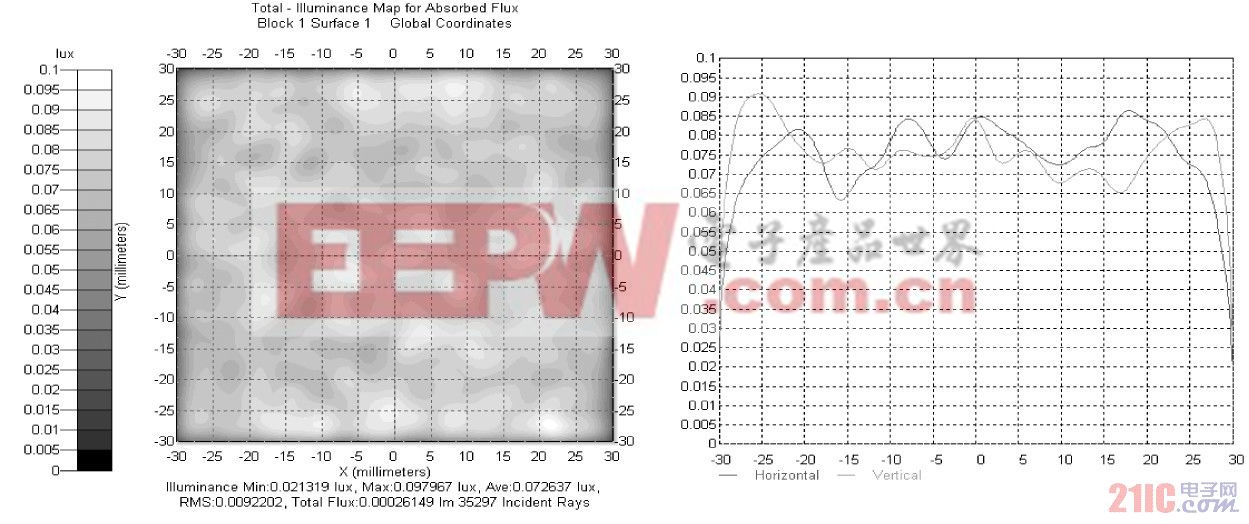
圖5 照度分布圖

　　4 結論

　　本文通過對微分方程的數值求解求出自由反射曲面的面型，依據不同的光源和照明需求得到不同的邊界條件和具體的方程，可自由設計反射曲面。

　　反射面型的配光結構可避免透鏡的加工成本高及對能量吸收率高等缺點。