基于數學優化法的帶通濾波器研究
加入技術交流群
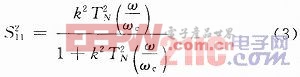
由式(2)，(3)可得，S11和S21的零點分別為ωzi，ωpi(i由N決定)。
設最終要實現的是中心頻率為ω0的帶通濾波器，現根據式(4)將低通響應轉換為帶通響應。
式中：△，ω0分別為帶通濾波器的相對帶寬和中心頻率；ωi'為低通響應的頻率點：ωi為低通響應轉換為帶通響應后ωi'的對應頻率點。
由式(4)有：
得到對應帶通濾波器中S11和S21的零點ωzi，ωpi，即所要求解的優化頻率點。
1．2 目標函數的構造
考慮到實際中介質損耗、原件損耗、尺寸誤差諸多方面的問題，在1．1中所提及的理想條件下的函數關系式(1)，(2)，(3)實際是不可實現的，由于PLR的零點就是反射函數S11的零點，而它的極點為傳輸函數S21的零點，因此可以選擇S11和S21的零點構造目標函數，至于常數k可以從ω=±1處的反射系數
計算得出，據此做出如下目標函數：
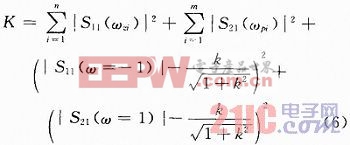
本文提出使用梯度優化算法來對目標函數逼近。首先求得目標函數K的梯度。為了使優化過程更為有效，采用目標函數的梯度來搜索其極值點。這種基于梯度的優化方法收斂極快，而且不會出現優化過程無法收斂或者收斂于局部極值點的情況，從而能夠快速而準確地逼近目標函數。
評論