摘要:數模轉換器的核心是一個精密R-2R梯形網絡，根據電路理論靈活運用DAC 中的梯形網絡，可以用DAC實現新的功能。給出了靈活運用DAC梯形網絡的兩種方法

1 概述

R-2R梯形網絡的DAC是最為常見的一種數模轉換器件，它的基本使用方法如圖1所示。

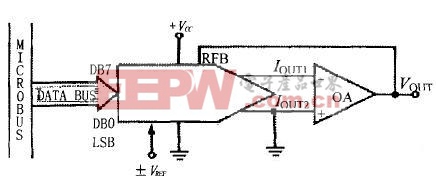
圖1 DAC的使用方法

倒置R-2R梯形網絡的DAC是由如圖2的一個倒置R-2R梯形網絡和由數碼控制的單刀雙置開關組成的。當像圖1那樣在梯形網絡之后級聯一個運算放大器，數碼控制的單刀雙置開關在兩個位置切換時不論那一邊的電位都是0。因此倒置R-2R梯形網絡的VREF端到地的電阻總是R，第i個單刀雙置開關上的電流為VREF/(2iR)經過運放后這個單刀雙置開關可以控制電壓為-VREF/2i (Rfb=R時)。

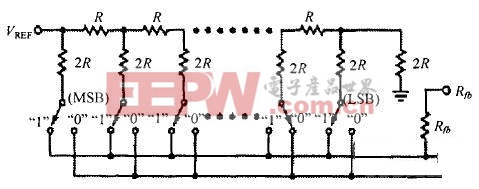
圖2 倒置R-2R梯形網絡的組成

2 反向使用DAC實現轉換模擬電壓的直接輸出

從圖1中可以看到，DAC最常見的使用方法是用電流作為轉換途徑的，這樣在DAC之后必須接一個運放將電流轉化為電壓才可以使用。而如果如圖3所示將DAC0832反過來使用，從兩個電流輸出端輸入電壓，即可直接從基準電壓輸入點直接得到轉換電壓，而無須再加一級運放。從參考電壓端得到的電壓為VREF×D/2n(D為數字輸入的值，n為DAC的位數)，現證明之。

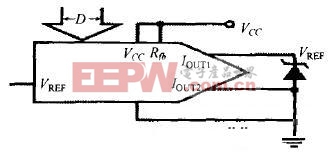
圖3反向使用DAC

當有一個或多個數碼控制的雙置開關放到“1”的位置時，它們與IOUT1連通即和高電平(Vin即Iout1端的電平)連通。根據線性電路的疊

加定理VREF端的電壓等于各個與高電平聯通的點分別與高電平聯通時VREF上的電壓之和。這個命題等價于當第p個開關放到“1”的位置時參考電壓腳輸出的電平Vp=2-p×Vin即可。當第P個開關(任意)與高電平聯通時電路如圖4所示。

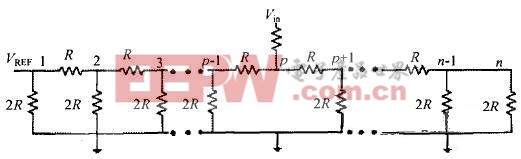
圖4當某個開關與高電平聯通時的電路

用數學歸納法證明之，假設上述命題成立。當最高位(MSB)與高電平接通時顯然最高位的右邊仍是一個梯形網絡，電阻為2R，故輸出電壓為2-1×Vin，滿足假設。當第P與高電平接通時，如圖4設梯形網絡中阻值為R的各個電阻之間的點為1，2，……，n，n-1這些以左的電阻對地的阻值為R1，R2，……，Rn。則可以得到Ri與Ri+1之間的遞推關系是：Ri+1等于(Ri+R)并聯上2R，即：

被接到高電平的電阻右邊的網絡阻值始終是2R，故總可以把它簡化為一個阻值為2R的電阻則：

根據歸納假設，當第p個電阻被接到Vin時，輸出電壓為：

Vp=2-p×Vin(3)

第p+1個電阻被接到Vin時，由式(2)得到Vp+1，再將式(2)代入Vp+1。得：

將式(3)代入式(4)化簡后有：

Vp+1=2-p+1Vin(4)

即證明歸納假設成立。