基于FPGA的FFT算法優化及其在磁共振譜儀中的應用
加入技術交流群
2 FFT算法實現
FFT算法在FPGA上實現的過程中，信號的值、系統的系數和運算中的結果都存儲在有限字長的存儲單元中，從而導致了設計時的無限精度轉變成實現時的有限精度，必將產生相對于原設計系統的誤差，嚴重時會將由于雙通道不平衡產生的鏡像峰湮滅，從而使整個設計失去意義。
為了實現FFT實時運算，基于FPGA的FFT信號處理模塊是關鍵，并且要求此模塊能在頻率至少為210 MHz的系統時鐘下穩定工作。同時又因為并行的FFT設計需要占用大量的資源，資源使用率過大會制約布局布線后的時序收斂。為了平衡資源與速度間的矛盾，整個設計通過64點FFT并行模塊的復用來實現。
2．1 有限字長效應及其優化措施
在FFT算法中，采用蝶形計算，如圖3所示。
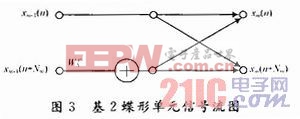
對于基2時間抽選FFT算法，蝶形公式如下：
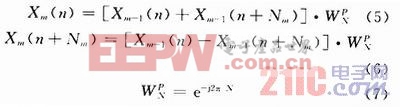
式中：N為FFT點數；Nm和P為兩個同迭代次數m有關的量；Xm-1為ADC輸出信號經過m-2級蝶形運算得到的計算結果；旋轉因子
由式(7)給出，每個蝶形包含兩個復數乘法。
由于存儲單元有限，必須對計算結果截取，進行定點化，但是同時又會引入舍入誤差en，這種現象即為有限字長效應。考慮到每個復數乘法相當于4個實數乘法，因此有限字長時復數乘法的實際乘積可以表示為：
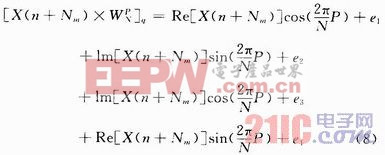
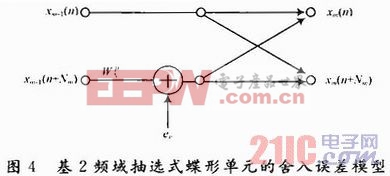
式中e1，e2，e3，e4分別為其對應的實數乘法的舍入誤差。因此可進一步建立如圖4所示的蝶形計算舍入誤差模型。
評論