Boost變換器的輸出電容
無論是Buck還Boost電路,因為輸出穩定的電壓是我們的需求,我們需要保障我們輸出電壓的穩定性,包括輸出紋波,以及負載變化的動態響應。
與輸入電容一樣,輸出電容的電壓紋波由電容電荷量變化和ESR決定。
1、電容電荷量變化引起的Vq
一個周期內,電容的充電電荷量和放電電荷量必然一樣。輸出電容放電時段的放電電量利用放電電流進行計算,此時就是看成輸出電容給負載獨立供電,如圖所示。放電電流就是負載電流,這里我們可以認為Iout是恒定的,為Iout=Vout/RLoad。

放電的電荷量等于容量乘以電容電壓的變化,也等于放電電流乘以放電時間,即:
Q=VqCout=IoutTon=Iout*T*D

2、ESR造成的壓降Vesr
在開關導通的時候,二極管不導通,負載的電流為Iout,完全由輸出濾波電容提供負載電流。在導通時間里面,輸出電容上的電流,我們認為是不變的。

在開關從導通切換到斷開時,電感的電流已經是充到最大的,因為先前開關導通時電感一直在充電,所以切換時電感電流最大,且等于電感平均電流加上紋波電流的一半,即為IL+△IL/2。
開關的狀態切換時,這個已經充好的電流會通過二極管給負載供電,負載電流為Iout。同時,電感還要給電容進行充電。根據基爾霍夫定律,節點電流和為0,那么電容的充電電流就是電感最大的電流IL+△IL/2減去負載的電流Iout,即IL+△IL/2-Iout。

在開關斷開之前,電容是放電狀態,此時電流為負值,電流值為-Iout。
在開關斷開之后,電容的狀態瞬間變成充電狀態,電流瞬間反向,為IL+△IL/2-Iout,并逐步降低。但是電流的峰值已經確定為IL+△IL/2-Iout。ESR的電流波形如圖所示。

那么ESR兩端的電壓ESR是電流與其阻值相乘Iesr*ESR。最大值(IL+△IL/2-Iout)*ESR,與最小值-Iout*ESR,兩者相減,就是ESR上電壓變化量的峰峰值,也是ESR產生的紋波電壓大小。

3、綜合Vesr和Vq計算紋波電壓
我們在假定負載不變化的情況下,我們可以認為電壓變化就是由ESR和電容上電量變化導致的,所以我們可以認為△Vout=Vesr+Vq,我們就可以獲得△Vout的表達式了,如果知道△Vout,我們也能得到輸出濾波電容Cout的大小或者是ESR了。

4、負載變化的情況
以上我們的分析都是基于負載不會變化的理想情況,但是實際電路中,我們的負載是會隨著用電器件的狀態而始終變化的。與Buck電路一樣,Boost變換器電路一樣需要考慮負載變化情況下的輸出電容的容值是否可以滿足需求。
(1)當負載電流瞬時增加之后,電感電流還來不及變化,那么此時輸出電容上的充電電流小于負載電流,電容電壓開始下降。
(2)電容電壓的下降,會導致電感電流的增加。電感電流增加之后,使得負載電容的充電電流開始增加,直到等于新的負載電流,但是在這個過程中,電容電壓還是下降的。
(3)電感電流持續增加,使得負載電容的充電電流開始大于新的負載電流,電容電壓開始上升。
(4)電容電壓逐漸恢復到最初的值,但是,電感電流還是在增加。當電容電壓恢復到初始值時,此時向其充電的電流大于負載電流,所以輸出電壓持續增加,開始大于初始值。而比初始值還大的輸出電壓最終又使得電感電流開始下降。
經過一段時間的振蕩之后,boost電路重新穩定在新的平衡點。
我們期望一個周期內,電容上因為負載電流突變導致的電壓的變化值不應該超過允許的電壓變化范圍。因為我們在計算電容放電的過程中,已經按照最大輸出負載進行計算了,如果這個過程中電流的變化,都是在最大輸出負載電流以下變化,所以對電容的容值只會更小。所以我們一般不會再考慮計算Boost電路中電容負載變化對容值需求。



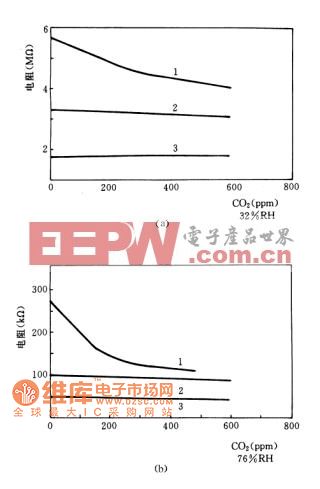


評論