鋰電池已被廣泛應用于工業、日常生活等領域，對電池荷電狀態（SOC）的估算已成為電池管理的重要環節。但是，由于電池結構復雜，電池的荷電狀態受放電電流、電池內部溫度、自放電、老化等因素的影響，使得SOC的估算困難。目前SOC估算方法有：開路電壓法、安時計量法、內阻法、神經網絡和卡爾曼濾波法。國外V. Pop等人提出EMF-SOC模型［1-2］，即電池電動勢與荷電狀態的關系模型來估算SOC，相當于開路電壓法，該方法用于電池靜置足夠長時間后進行估計，不能實時估計；也有人采用安時計量法或卡爾曼濾波法估計SOC，安時計量法由于電流波動較大或測量誤差長時間積累導致估計不精確；卡爾曼濾波法則在建立準確實用的電池動態模型上存在很大困難，為此本文根據鋰電池在應用中的實際情況，采用了一種新思路來估算SOC，即將電池的工作狀況分為三種狀態，對每種狀態的SOC逐一進行估算，在估算過程中消除影響SOC的因素，且使三種狀態下SOC的值互為前提，從而提高SOC的估算精度。

　　1、電池工作狀態及SOC估計

　　電池狀態根據實際情況可分為三種狀態，這里將其定義為靜止、恢復、充放電，它們的關系如圖1。

　　圖1 電池工作狀態圖

　　1.1 靜止狀態

　　電池的靜止狀態是指電池工作停止后，完全恢復了的狀態，從恢復狀態轉化而來，可直接轉入充放電狀態，此狀態下SOC的計算量作為充放電狀態下SOC估算的初始值。由于此狀態下的特點是電流為零、無極化現象，其SOC值與開路電壓有很好的對應關系，因此能用開路電壓法直接估算電池的SOC值，電池的開路電壓與SOC值的關系曲線如圖2。

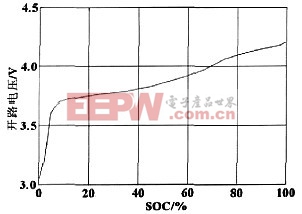
　　圖2 電池的開路電壓與SOC值的關系曲線

　　在靜止狀態下，電池容量主要受自放電現象的影響使得電池電量會隨著時間的增加而減少，而用開路電壓與SOC值的對應關系來估算SOC，本身就可以消除自放電引起的電量損失的影響，從而能使SOC值更加準確地反映電池的狀態。

　　1.2 恢復狀態

　　恢復狀態是指電池從放電或充電狀態轉到靜止狀態的過渡階段。一般這個階段經歷的時間為8h（此值為經驗值），此狀態下SOC的計算量作為充放電狀態下SOC估算的初始值，這時的SOC估算主要考慮放電或充電結束后電池電量的改變量。從放電或充電狀態進入恢復狀態后電池電量會隨時間增加而有所增加，其變化的原因是在放電或充電過程中電池內部產生極化現象，部分電量沒有用于實際的充放電中而是慢慢累積起來，當電池停止工作后極化現象會慢慢消失，累積的電量也會恢復。

　　恢復階段SOC的估算：

　　（a）若從放電狀態進入恢復狀態

　　SOCt=SOCd+M×t/（8×Q）×100%

　　式中：SOCt為恢復狀態下的荷電狀態值；SOCd為放電狀態終止時的荷電狀態值；M為在電池放電過程中的累積電量（可以恢復）；t為電池在恢復狀態下經歷的時間；Q為電池的實際容量。

　　（b）若從充電狀態進入恢復狀態

　　SOCt=SOCc+M×t/（8×Q）×100%

　　式中：SOCt為恢復狀態下的荷電狀態值；SOCc為充電狀態終止時的荷電狀態值；M為在電池充電過程中的累積電量（可以恢復）；t為電池在恢復狀態下經歷的時間；Q為電池的實際容量。

　　M值的計算：

　　（a）放電狀態下

　　若η2>η1，

　　Mt+Δt=Mt+I2×Δt×（1-η2）/η2-I1×Δt×（η2-η1）/η1×η2（1）

　　推導如下：

　　t+Δt時刻，安時計量法計算的電量：I2×Δt;

　　t+Δt 時刻，電池實際放出的電量：I2×Δt/η2;

　　t+Δt時刻，電池損失電量：I2×Δt ×（1-η2）/η2;

　　t時刻，I1放電時，由于η2>η1，損失電量I1×Δt×（1-η1）/η1較大，在t+Δt 時刻就會恢復少許電量，恢復量為：

　　I1×Δt×（1-η1）/η1-I1×Δt×（1-η2）/η2

　　即I1×Δt ×（η2-η1）/η1×η2

　　若η1≥η2，t+Δt時刻損失的電量更大，因此就無恢復量I1×Δt ×（η2-η1）/η1×η2.

　　Mt +Δt=Mt+I2×Δt ×（1-η2）/η2 （2）。

　　式中：η1、I1為電池在t時刻的放電庫侖效率和電流，η2、I2為電池在t +Δt 時刻的放電庫侖效率和電流。

　　（b）充電狀態下，充電方式一般為恒流恒壓方式，因此庫侖效率、電流值的變化較放電狀態下穩定。

　　恒流階段，電流恒定，而電池溫度會有所增加：

　　M t +Δt=Mt+I×Δt ×（1+η1-2η2）

　　公式推導同（1）。

　　式中：I為恒流階段的電流值；η1、η2為恒流階段的充電庫倫效率，η2>η1，它們的差別是由溫度引起的。恒壓階段，電流會隨電壓的升高而降低。

　　若η2>η1，Mt +Δt=Mt+I2×Δt×（1-η2）-I1×Δt ×（η2-η1）公式推導同（1）。

　　若η1≥η2，Mt+Δt=Mt+I2×Δt×（1-η2）公式推導同（2）。

　　式中：η1、I1為電池在t時刻的充電庫侖效率和電流；η2、I2為電池在t +Δt 時刻的充電庫侖效率和電流。

　　在充電情況下，一般用已規定好的電流進行充電，可認為η=1.

　　1.3 充電或放電狀態

　　1.3.1 安時計量法的改進。

　　此狀態下在SOC估算時一般采用安時計量法，即Q=∫IDT，但這種方法由于沒有考慮庫侖效率，使得計算結果隨著時間的積累誤差會越來越大。為此，本文對安時計量法進行了改進，在充放電過程SOC估算中增加了庫侖效率因子以及以其為基礎計算出的動態恢復電量部分，從而提高了安時計量法的準確性。

　　改進后的SOC計算公式如下所示：

　　（a）充電時。

　　若η2>η1：

　　等式右邊第二項表示實際充入電池的電量部分，第三項表示電池充電過程中動態恢復的電量部分。

　　若η1≥η2：

　　（b）放電時。

　　若η2>η1：

　　等式右邊第二項表示實際放出的電池電量部分，第三項表示電池放電過程中動態恢復的電量部分。

　　若η1≥η2：