在超大規(guī)模集成電路（VLSI）設(shè)計(jì)中，時鐘域交叉過程必然會出現(xiàn)亞穩(wěn)態(tài)現(xiàn)象。要實(shí)現(xiàn)魯棒且高可靠性的電路設(shè)計(jì)，必須對亞穩(wěn)態(tài)進(jìn)行抑制。想要掌握亞穩(wěn)態(tài)的解決方法，以及如何設(shè)計(jì)滿足指標(biāo)要求的同步器，我們需要明確其產(chǎn)生原因、影響因素，以及降低其發(fā)生概率的方式。

亞穩(wěn)態(tài)與觸發(fā)器同步器

為了更深入理解時序元件進(jìn)入亞穩(wěn)態(tài)的過程，以及亞穩(wěn)態(tài)的消解時長，可參考圖 1。

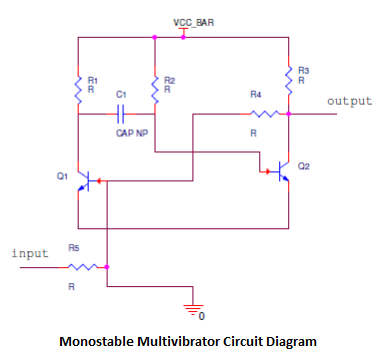
圖 1：典型的主從鎖存器觸發(fā)器電路

圖 1 為典型的主從鎖存器觸發(fā)器電路，由主鎖存器和從鎖存器組成，每個鎖存器均包含兩個級聯(lián)的反相器。在正常且正確的工作狀態(tài)下，時鐘為低電平時，傳輸門 T₁ 導(dǎo)通，輸入信號 D 傳入主鎖存器中由反相器 I₁ 和 I₂ 構(gòu)成的閉環(huán)電路。

當(dāng)時鐘信號上升沿到來時，傳輸門 T₁ 關(guān)斷、T₂ 導(dǎo)通，主鎖存器中經(jīng)過整形的輸入信號隨后傳入從鎖存器，經(jīng)過一個觸發(fā)器傳播延遲（T_PCQ）后，信號最終在輸出端 Q 穩(wěn)定輸出。

若假設(shè)時鐘為低電平時，輸入信號 D 和節(jié)點(diǎn) A 的邏輯狀態(tài)為 1，節(jié)點(diǎn) B 的邏輯狀態(tài)為 0；當(dāng)輸入信號 D 跳轉(zhuǎn)為邏輯 0 時，節(jié)點(diǎn) A 的電壓開始下降，節(jié)點(diǎn) B 的電壓則隨之上升。

若輸入信號 D 的跳變發(fā)生在時鐘有效沿附近，傳輸門 T₁ 會在節(jié)點(diǎn) A 和節(jié)點(diǎn) B 完成 0、1 邏輯狀態(tài)的跳變前關(guān)斷，此時兩個節(jié)點(diǎn)可能進(jìn)入亞穩(wěn)態(tài)，被鎖定在 1 和 0 之間的中間電壓值，需要耗費(fèi)不確定的時間，才能隨機(jī)穩(wěn)定至 0 或 1 其中一個邏輯狀態(tài)。

亞穩(wěn)態(tài)建模

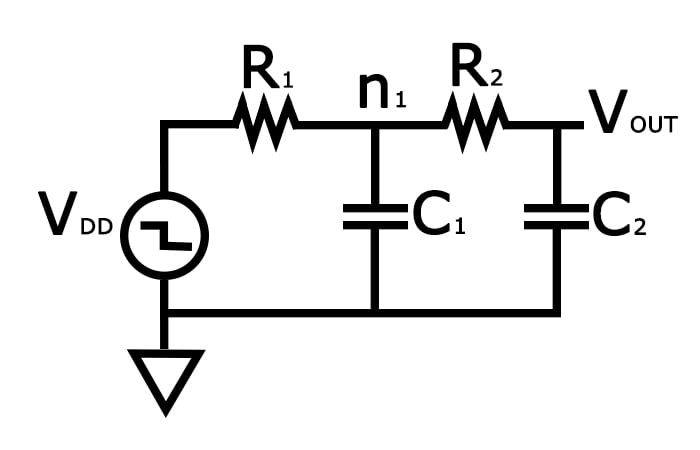
為了更清晰地理解亞穩(wěn)態(tài)，以及鎖存器穩(wěn)定并脫離亞穩(wěn)態(tài)所需的時間，我們將反相器建模為增益為 G 的負(fù)放大器，驅(qū)動傳輸門和另一個反相器的電阻 R 與容性負(fù)載 C（見圖 2）。為簡化分析，假設(shè)反相器的 PMOS 管和 NMOS 管驅(qū)動能力相同、閾值電壓一致，中點(diǎn)電壓 V_m = 電源電壓 V_DD/2，隨后求解節(jié)點(diǎn) A 和節(jié)點(diǎn) B 之間的電壓差。

圖 2：初始電壓差隨時間變化曲線

根據(jù)文獻(xiàn) ，該系統(tǒng)可通過如下公式建模：

其中，ΔV_in 為時鐘有效沿切斷輸入 D 與節(jié)點(diǎn) A 的連接時，節(jié)點(diǎn) A 和節(jié)點(diǎn) B 之間的電壓差；ΔV_out 為經(jīng)過時間 t 后，兩個節(jié)點(diǎn)之間的電壓差。

對于初始電壓差為 ΔV_in 的情況，節(jié)點(diǎn) A 和節(jié)點(diǎn) B 的電壓差達(dá)到電源電壓 V_DD、亞穩(wěn)態(tài)完成消解（即兩個節(jié)點(diǎn)穩(wěn)定至 0 或 1 邏輯狀態(tài)）所需的時間 t_d，可由以下公式得出：

圖 3 展示了初始電壓差與亞穩(wěn)態(tài)消解時間之間的關(guān)系。

圖 3：輸入電壓差與亞穩(wěn)態(tài)消解時間的關(guān)系曲線

當(dāng)初始電壓差 ΔV_in 較大時，節(jié)點(diǎn) A 和節(jié)點(diǎn) B 能快速穩(wěn)定至對應(yīng)的 1 和 0 邏輯狀態(tài)；當(dāng)初始電壓差 ΔV_in 極小時，亞穩(wěn)態(tài)的消解則需要耗費(fèi)較長時間。公式 1 表明，輸出電壓差 ΔV_out 由初始電壓差 ΔV_in 決定。

圖 3 的上半部分曲線看似有違直覺，這是因?yàn)橹笖?shù)增長發(fā)生在極小的數(shù)值范圍內(nèi)；下半部分曲線則更具直觀性，其以對數(shù)尺度描繪了節(jié)點(diǎn)間的電壓差變化。

公式 2 同時表明，若初始輸入電壓差為 0（例如節(jié)點(diǎn) A 和節(jié)點(diǎn) B 的電壓均為 0.5V），亞穩(wěn)態(tài)的消解將耗費(fèi)無限長的時間。但這一情況無需過度擔(dān)憂，即便時鐘上升沿切斷輸入信號時，兩個節(jié)點(diǎn)的電壓均為 0.5V，微小的熱噪聲也會打破這一平衡，最終使亞穩(wěn)態(tài)得以消解。

綜上，當(dāng)數(shù)據(jù)在相位或頻率不同的兩個時鐘域之間傳輸時，異步信號可能在采樣時鐘的跳變沿發(fā)生翻轉(zhuǎn)，導(dǎo)致輸出端進(jìn)入亞穩(wěn)態(tài)，在 0 和 1 之間的中間值震蕩，直至經(jīng)過公式 2 計(jì)算的 t_d 時間后，才會隨機(jī)穩(wěn)定至某一邏輯狀態(tài)。至關(guān)重要的是，亞穩(wěn)態(tài)必須在信號進(jìn)入任何組合邏輯前穩(wěn)定至有效邏輯值，以避免亞穩(wěn)態(tài)在邏輯鏈路中傳播。

進(jìn)入亞穩(wěn)態(tài)的概率

明確亞穩(wěn)態(tài)無法避免，且知曉其消解所需時間后，我們接下來分析電路進(jìn)入亞穩(wěn)態(tài)的初始概率，以及在規(guī)定時間內(nèi)無法消解亞穩(wěn)態(tài)、進(jìn)而導(dǎo)致邏輯失效的概率。

設(shè)時鐘周期為 T_C，若數(shù)據(jù)輸入在孔徑時間 T_A 內(nèi)發(fā)生變化，就會引發(fā)亞穩(wěn)態(tài)現(xiàn)象。那么電路進(jìn)入亞穩(wěn)態(tài)的概率，即為可能進(jìn)入亞穩(wěn)態(tài)的時間與總時間的比值，計(jì)算公式如下：

其中，F(xiàn)_C 為設(shè)計(jì)的時鐘頻率。由于輸入信號 D 并非每個時鐘周期都會發(fā)生變化，定義每秒內(nèi)的信號跳變速率為 F_D（即進(jìn)入亞穩(wěn)態(tài)的速率），則有：

電路進(jìn)入亞穩(wěn)態(tài)的平均間隔時間為：

以一個時鐘頻率為 2GHz 的設(shè)計(jì)為例，若觸發(fā)器的建立時間為 15 皮秒、保持時間為 5 皮秒，其進(jìn)入亞穩(wěn)態(tài)的概率為 0.04；若輸入信號的跳變速率為 400MHz（0.4×10⁹），則該鎖存器每秒會進(jìn)入 16×10⁶ 次亞穩(wěn)態(tài)，即每 125 個時鐘周期就會出現(xiàn)一次亞穩(wěn)態(tài)，發(fā)生頻率極高。

要計(jì)算亞穩(wěn)態(tài)的失效概率，需先定義消解時間 T_r：主鎖存器必須在該時間內(nèi)完成節(jié)點(diǎn) A 和 B 的狀態(tài)穩(wěn)定，避免亞穩(wěn)態(tài)傳播至從鎖存器。主鎖存器的消解時間 T_r,master 為半個時鐘周期減去從鎖存器的建立時間，而從鎖存器的建立時間等于觸發(fā)器的傳播延遲 T_PCQ（即信號通過傳輸門 T₂ 和反相器 I₃ 的延遲），計(jì)算公式為：

主鎖存器亞穩(wěn)態(tài)消解失效的概率，等于電路進(jìn)入亞穩(wěn)態(tài)的概率，乘以在消解時間 T_r 內(nèi)無法完成亞穩(wěn)態(tài)消解的概率，即：

亞穩(wěn)態(tài)消解失效的概率推導(dǎo)方式與亞穩(wěn)態(tài)發(fā)生概率 P (MS) 一致。結(jié)合公式 1，假設(shè)完成亞穩(wěn)態(tài)消解需要的最小初始電壓差為 ΔV_in,min，且所有可能的 ΔVin 取值概率均等，那么在消解時間 T_r 內(nèi)無法完成亞穩(wěn)態(tài)消解的概率為：

由此可得整體失效概率為：

對應(yīng)的平均失效間隔時間（MTBF）為：

觸發(fā)器的失效概率計(jì)算，需同時考慮主鎖存器進(jìn)入亞穩(wěn)態(tài)且消解失效的概率，以及從鎖存器的相關(guān)概率，計(jì)算公式為：

其中，從鎖存器的消解時間 T_r,slave為：

式中，t_setup 為第二個觸發(fā)器的建立時間，t_pd 為從第一個觸發(fā)器的從鎖存器輸出，到第二個觸發(fā)器輸入的級聯(lián)延遲。觸發(fā)器完成亞穩(wěn)態(tài)消解所需的總時間 T_r,flop 可表示為：

若主從鎖存器為相同規(guī)格的觸發(fā)器，則 T_r,flop 的計(jì)算公式為：

由此可得單級觸發(fā)器同步器的失效概率為：

假設(shè)時間常數(shù) τ=35 皮秒，級聯(lián)延遲 t_pd=0，那么 T_r,flop =500 - (2×15)=470 皮秒。上述同步器的失效概率為 58.9×10^-9，失效速率為 23.6 次 / 秒，對應(yīng)的平均失效間隔時間由以下公式計(jì)算：

計(jì)算得平均失效間隔時間為 42.4 毫秒，該數(shù)值極低，意味著同步器極易失效。

綜上，當(dāng)數(shù)據(jù)在不同時鐘域間傳輸時，進(jìn)入亞穩(wěn)態(tài)的概率可由公式 3 計(jì)算，觸發(fā)器輸出會在公式 2 計(jì)算的 td 時間內(nèi)處于不穩(wěn)定狀態(tài)，直至亞穩(wěn)態(tài)消解。

觸發(fā)器同步器設(shè)計(jì)

若單級觸發(fā)器同步器的亞穩(wěn)態(tài)消解時間 t_d 超過一個時鐘周期，無法在該時間內(nèi)完成消解，或其平均失效間隔時間過短，可通過增加觸發(fā)器級數(shù)的方式優(yōu)化。增加級數(shù)能延長同步器在亞穩(wěn)態(tài)傳播至后續(xù)邏輯鏈路前的總消解時間  T_r,sync ，最終降低整體失效概率，提升平均失效間隔時間。

對于 n 級同步器，其失效概率為前序同步器級消解失效的概率，乘以最后一級同步器的失效概率，計(jì)算邏輯與公式 4 一致。若使用規(guī)格相同的觸發(fā)器，且單級消解時間均為 T_r，則只需將指數(shù)項(xiàng)乘以同步器的級數(shù)即可。n 級同步器的失效概率和平均失效間隔時間計(jì)算公式為：

在上述示例中，若增加一級同步器，平均失效間隔時間將提升至 8 小時；若再增加一級，平均失效間隔時間可達(dá) 621 年。可見，由于亞穩(wěn)態(tài)消解時間出現(xiàn)在指數(shù)項(xiàng) e 中，同步器的平均失效間隔時間會呈指數(shù)級增長。

當(dāng)計(jì)算得出的平均失效間隔時間達(dá)到 600 年左右時，看似系統(tǒng)已處于安全狀態(tài)，亞穩(wěn)態(tài)引發(fā)的系統(tǒng)失效會在很久后才發(fā)生，但實(shí)際情況并非如此。

設(shè)計(jì)中同步器的總數(shù)量，會直接影響系統(tǒng)的整體平均失效間隔時間。若單個同步器的平均失效間隔時間為 600 年，但設(shè)計(jì)中包含 600 個同步器，那么系統(tǒng)的實(shí)際平均失效間隔時間僅為 1 年，即每年都可能有一個同步器發(fā)生失效。

因此，在進(jìn)行系統(tǒng)和同步器架構(gòu)設(shè)計(jì)時，必須考慮同步器的使用數(shù)量，并計(jì)算其對系統(tǒng)整體平均失效間隔時間的影響，以避免突發(fā)失效。包含 K 個同步器的系統(tǒng)，其整體平均失效間隔時間計(jì)算公式為：

總結(jié)

由于時鐘域交叉過程中的亞穩(wěn)態(tài)現(xiàn)象無法避免，抑制其影響對保證設(shè)計(jì)可靠性至關(guān)重要。明確設(shè)計(jì)進(jìn)入亞穩(wěn)態(tài)的概率及其失效概率，是選擇或設(shè)計(jì)高平均失效間隔時間同步器的核心，唯有如此，才能確保電路設(shè)計(jì)的可靠性和魯棒性。